【题目】如图,已知AB∥ED,设∠A+∠E=α,∠B+∠C+∠D=β,则( )

A. α-β=0B. 2α-β=0C. α-2β=0D. 3α-2β=0
参考答案:
【答案】B
【解析】
过点C作CF∥AB,根据平行的传递性可得CF∥ED,由平行线的性质:两直线平行,同旁内角互补,得∠D+∠ DCF=180°,∠B+∠ BCF=180°,∠A+∠ E=180°,从而可得2α-β=0.
过点C作CF∥AB,如图,
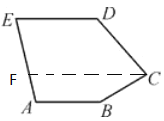
∵AB∥ ED,CF∥ AB,
∴CF∥ED,
∴∠ D+∠ DCF=180°,
∵CF∥AB,
∴∠ B+∠ BCF=180°,
∴∠ β=∠ B+∠ BCD+∠ D=∠ B+∠ B CF+∠ DCF+∠ D=360°,
∵AB∥ED,
∴∠A+∠ E=180°,
∴2α-β=0.
故答案为:B.
-
科目: 来源: 题型:
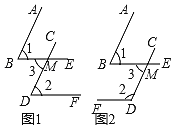
查看答案和解析>>【题目】如果一个角的两边与另一个角的两边分别平行,某同学为了探究这两个角的关系,画出来以下两个不同的图形,请你根据图形完成以下问题:
(1)如图1,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是 ;
如图2,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是 ;
(2)根据(1)的探究过程,我们可以得到结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是 ;
(3)利用结论解决问题:如果有两个角的两边分别平行,且一个角比另一个角的3倍少40°,则这两个角分别是多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数
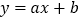 与二次函数
与二次函数 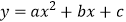 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
A.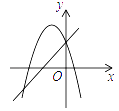
B.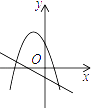
C.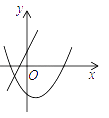
D.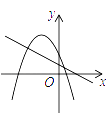
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )

A.3m
B. m
m
C. m
m
D.4m -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).

①将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
②将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
③直接写出点B2 , C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】对代数式
 ,老师要求任意取一个x的值后求出代数式的值.圆圆发现,大家所求得的代数式的值都大于等于0,即x=-3时代数式的最小值是0.利用这个发现,圆圆试着写出另外一些结论:①在x=-3时,代数式(x+3)2+2的最小值为2;②在a=-b时,代数式(a+b)2+m的最小值为m;③在c=-d时,代数式-(c+d)2+n的最大值为n;④在
,老师要求任意取一个x的值后求出代数式的值.圆圆发现,大家所求得的代数式的值都大于等于0,即x=-3时代数式的最小值是0.利用这个发现,圆圆试着写出另外一些结论:①在x=-3时,代数式(x+3)2+2的最小值为2;②在a=-b时,代数式(a+b)2+m的最小值为m;③在c=-d时,代数式-(c+d)2+n的最大值为n;④在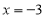 时,代数式
时,代数式 的最大值为29.其中正确的为( )
的最大值为29.其中正确的为( )A. ①②③B. ①③C. ①④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆实验外国语学校运动会期间,小明和小欢两人打算匀速从教室跑到600米外的操场参加入场式,出发时小明发现鞋带松了,停下来系鞋带,小欢继续跑往操场,小明系好鞋带后立即沿同一路线开始追赶小欢.小明在途中追上小欢后继续前行,小明到达操场时入场式还没有开始,于是小明站在操场等待,小欢继续前往操场.设小明和小欢两人相距
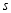 (米),小欢行走的时间为
(米),小欢行走的时间为 (分钟),
(分钟),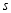 关于
关于 的函数图像如图所示,则在整个运动过程中,小明和小欢第一次相距
的函数图像如图所示,则在整个运动过程中,小明和小欢第一次相距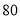 米后,再过_____分钟两人再次相距
米后,再过_____分钟两人再次相距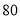 米.
米.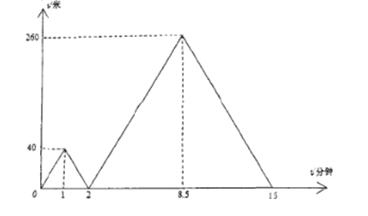
相关试题

