【题目】如图,正方形网格中的每个小正方形的边长都是![]() ,每个小括的顶点叫做格点.
,每个小括的顶点叫做格点.
(![]() )如图
)如图![]() ,点
,点![]() ,
,![]() ,
,![]() 是小正方形的顶点,直接写出
是小正方形的顶点,直接写出![]() 的度数.
的度数.
(![]() )在图
)在图![]() 中以格点为顶点画一个面积为
中以格点为顶点画一个面积为![]() 的正方形.
的正方形.
(![]() )在图
)在图![]() 中以格点为顶点画一个三角形,使三角形三边长分别为
中以格点为顶点画一个三角形,使三角形三边长分别为![]() ,
,![]() ,
,![]() .
.
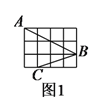
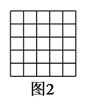

参考答案:
【答案】(![]() )
)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)连接AC,由勾股定理不难得出AC=BC=![]() ,∠ACB=90°,所以∠ABC=45°;(2)要画面积为10的正方形,即要画一个边长为
,∠ACB=90°,所以∠ABC=45°;(2)要画面积为10的正方形,即要画一个边长为![]() 的正方形,网格中连接长为3,宽为1的矩形的对角线,即可到长度为
的正方形,网格中连接长为3,宽为1的矩形的对角线,即可到长度为![]() 的线段,画出正方形即可;(3)首先画出长为2的线段,再分别画出长度为
的线段,画出正方形即可;(3)首先画出长为2的线段,再分别画出长度为![]() 、
、![]() 的线段,网格中连接长度为2宽度为1的矩形对角线即得到长度为
的线段,网格中连接长度为2宽度为1的矩形对角线即得到长度为![]() 的线段,连接长度为3宽度为2的矩形对角线即得到长度为
的线段,连接长度为3宽度为2的矩形对角线即得到长度为![]() 的线段,画出三角形即可.
的线段,画出三角形即可.
试题解析:
(![]() )
)

∠ABC=45°;
(![]() )如图所示:
)如图所示:

(![]() )如图所示:
)如图所示:

-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值: (2x-3y)2-(2x+y)(2x-y), 其中x=-1, y=-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】2010年5月27日,上海世博会参观人数达到37.7万人,这个数用科学记数法表示为( )
A.0.377×106人
B.3.77×105人
C.3.77×104人
D.377×103人 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=
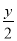 ,把x=
,把x= ,代入已知方程,
,代入已知方程,得(
 )2 +
)2 + ﹣1=0.
﹣1=0.化简,得y2+2y﹣4=0,
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+2x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b为有理数,a>0,b<0,且|a|<|b|,则a,b,-a,︱b︱的大小关系是( )
A.b<-a<︱b︱<a
B.b<-a<a<︱b︱
C.b<︱b︱<-a<a
D.-a<︱b︱<b<a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.
(1)若AE=2,求EC的长;
(2)若点G在DC上,且∠AGC=120°,求证:AG=EG+FG.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

相关试题

