【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

参考答案:
【答案】(1)证明见解析(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
【解析】试题分析:(1)根据矩形的有三个角是直角的四边形是矩形,已知CE⊥AN,AD⊥BC,所以求证∠DAE=90°,可以证明四边形ADCE为矩形.
(2)根据正方形的判定,我们可以假设当AD=![]() BC,由已知可得,DC=
BC,由已知可得,DC=![]() BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
BC,由(1)的结论可知四边形ADCE为矩形,所以证得,四边形ADCE为正方形.
试题解析:(1)证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE,
∴∠DAE=∠DAC+∠CAE=![]() ×180°=90°,
×180°=90°,
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
(2)当△ABC满足∠BAC=90°时,四边形ADCE是一个正方形.
理由:∵AB=AC,
∴∠ACB=∠B=45°,
∵AD⊥BC,
∴∠CAD=∠ACD=45°,
∴DC=AD,
∵四边形ADCE为矩形,
∴矩形ADCE是正方形.
∴当∠BAC=90°时,四边形ADCE是一个正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是
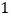 ,每个小括的顶点叫做格点.
,每个小括的顶点叫做格点.(
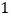 )如图
)如图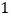 ,点
,点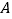 ,
,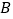 ,
, 是小正方形的顶点,直接写出
是小正方形的顶点,直接写出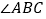 的度数.
的度数.(
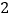 )在图
)在图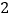 中以格点为顶点画一个面积为
中以格点为顶点画一个面积为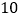 的正方形.
的正方形.(
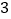 )在图
)在图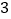 中以格点为顶点画一个三角形,使三角形三边长分别为
中以格点为顶点画一个三角形,使三角形三边长分别为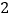 ,
,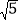 ,
,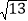 .
.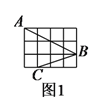
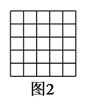

-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b为有理数,a>0,b<0,且|a|<|b|,则a,b,-a,︱b︱的大小关系是( )
A.b<-a<︱b︱<a
B.b<-a<a<︱b︱
C.b<︱b︱<-a<a
D.-a<︱b︱<b<a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.
(1)若AE=2,求EC的长;
(2)若点G在DC上,且∠AGC=120°,求证:AG=EG+FG.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①如果两个数的和为1,则这两个数互为倒数;②如果两个数积为0,则至少有一个数为0;③绝对值是本身的有理数只有0;④倒数是本身的数是-1,0,1。其中错误的个数是( )
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】若把每月生300个零件记作0个,则二月份生产了340个零件记作个,四月份生了280个零件记作个;
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于-4且小于3的所有整数的和是 。
相关试题

