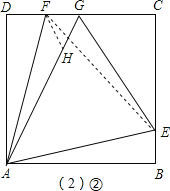
【题目】如图,在正方形ABCD中,点E、点F分别在边BC、DC上,BE=DF,∠EAF=60°.
(1)若AE=2,求EC的长;
(2)若点G在DC上,且∠AGC=120°,求证:AG=EG+FG.

参考答案:
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】试题分析:(1)连接EF,根据正方形的性质求出AB=AD,∠B=∠D,然后利用“边角边”证明△ABE和△ADF全等,根据全等三角形对应边相等可得AE=AF,从而得到△AEF是等边三角形,根据等边三角形的三条边都相等可得EF,再判断出△CEF是等腰直角三角形,根据等腰直角三角形的直角边与斜边的关系求解即可;
(2)在AG上截取GH=FG,可得△FGH是等边三角形,根据等边三角形的性质可得FH=FG,∠FHG=60°,再求出∠AFH=∠EFG,然后利用“边角边”证明△AFH和△EFG全等,根据全等三角形对应边相等AH=GE,然后证明即可.
试题解析:(1)解:如图,连接EF,
在正方形ABCD中,AB=AD,∠B=∠D,
在△ABE和△ADF中, 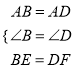 ,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∴EF=AE=2,
∵BE=DF,BC=CD,
∴BC﹣BE=CD﹣DF,
即CE=CF,
∴△CEF是等腰直角三角形,
∴EC=![]() EF=
EF=![]() ×2=
×2=![]() ;
;
(2)如图(2)②在AG上截取GH=FG,
∵∠AGC=120°,
∴∠AGF=60°,
∴△FGH是等边三角形,
∴FH=FG,∠FHG=60°,
∵△AEF是等边三角形,
∴∠AFE=60°,
∴∠AFE=∠GFH=60°,
∴∠AFE﹣∠EFH=∠GFH﹣∠EFH,
即∠AFH=∠EFG,
在△AFH和△BFG中, 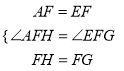 ,
,
∴△AFH≌△EFG(SAS),
∴AH=GE,
∴AG=AH+GH=EG+FG,
即AG=EG+FG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=
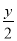 ,把x=
,把x= ,代入已知方程,
,代入已知方程,得(
 )2 +
)2 + ﹣1=0.
﹣1=0.化简,得y2+2y﹣4=0,
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+2x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是
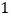 ,每个小括的顶点叫做格点.
,每个小括的顶点叫做格点.(
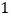 )如图
)如图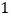 ,点
,点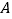 ,
,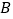 ,
, 是小正方形的顶点,直接写出
是小正方形的顶点,直接写出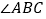 的度数.
的度数.(
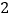 )在图
)在图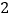 中以格点为顶点画一个面积为
中以格点为顶点画一个面积为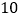 的正方形.
的正方形.(
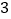 )在图
)在图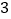 中以格点为顶点画一个三角形,使三角形三边长分别为
中以格点为顶点画一个三角形,使三角形三边长分别为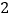 ,
,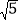 ,
,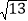 .
.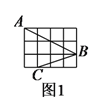
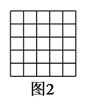

-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b为有理数,a>0,b<0,且|a|<|b|,则a,b,-a,︱b︱的大小关系是( )
A.b<-a<︱b︱<a
B.b<-a<a<︱b︱
C.b<︱b︱<-a<a
D.-a<︱b︱<b<a -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①如果两个数的和为1,则这两个数互为倒数;②如果两个数积为0,则至少有一个数为0;③绝对值是本身的有理数只有0;④倒数是本身的数是-1,0,1。其中错误的个数是( )
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】若把每月生300个零件记作0个,则二月份生产了340个零件记作个,四月份生了280个零件记作个;
相关试题

