搜索
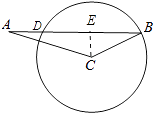
【题目】如图，在△ABC中，已知∠ACB=130°，∠BAC=20°，BC=2，以点C为圆心，CB为半径的圆交AB于点D，则BD的长为 ． 
参考答案：
【答案】
【解析】解：如图，作CE⊥AB于E． ∵∠B=180°﹣∠A﹣∠ACB=180°﹣20°﹣130°=30°，
在RT△BCE中，∵∠CEB=90°，∠B=30°，BC=2，
∴CE= 
BC=1，BE= 
CE= ，
∵CE⊥BD，
∴DE=EB，
∴BD=2EB=2 ．
故答案为2 ．
如图，作CE⊥AB于E，在RT△BCE中利用30度性质即可求出BE，再根据垂径定理可以求出BD．本题考查垂径定理、三角形内角和定理等知识，解题的关键是根据垂径定理添加辅助线，记住直角三角形30度角性质，属于基础题，中考常考题型．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，点C、D在⊙O上，∠A=2∠BCD，点E在AB的延长线上，∠AED=∠ABC
（1）求证：DE与⊙O相切；
（2）若BF=2，DF=
，求⊙O的半径． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小明遇到这样一个问题：如图1，△ABC中，AB=AC，点D在BC边上，∠DAB=∠ABD，BE⊥AD，垂足为E，求证：BC=2AE．
小明经探究发现，过点A作AF⊥BC，垂足为F，得到∠AFB=∠BEA，从而可证△ABF≌△BAE（如图2），使问题得到解决．
（1）根据阅读材料回答：△ABF与△BAE全等的条件是 AAS（填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个）
参考小明思考问题的方法，解答下列问题：
（2）如图3，△ABC中，AB=AC，∠BAC=90°，D为BC的中点，E为DC的中点，点F在AC的延长线上，且∠CDF=∠EAC，若CF=2，求AB的长；
（3）如图4，△ABC中，AB=AC，∠BAC=120°，点D、E分别在AB、AC边上，且AD=kDB（其中0＜k＜
），∠AED=∠BCD，求 
的值（用含k的式子表示）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，抛物线y=x2+
与y轴相交于点A，点B与点O关于点A对称
（1）填空：点B的坐标是；
（2）过点B的直线y=kx+b（其中k＜0）与x轴相交于点C，过点C作直线l平行于y轴，P是直线l上一点，且PB=PC，求线段PB的长（用含k的式子表示），并判断点P是否在抛物线上，说明理由；
（3）在（2）的条件下，若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上，求此时点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，一条直线与反比例函数y=
（x＞0）的图象交于两点A、B，与x轴交于点C，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数y= 
（x＞0）的图象交于两点D、E，连接DE，则四边形ABED的面积为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：2sin30°+3﹣1+（
﹣1）0﹣ 
． -
科目： 来源： 题型：
查看答案和解析>>【题目】某校对七、八、九年级的学生进行体育水平测试，成绩评定为优秀、良好、合格、不合格四个等第．为了解这次测试情况，学校从三个年级随机抽取200名学生的体育成绩进行统计分析．相关数据的统计图、表如下：
各年级学生成绩统计表
优秀
良好
合格
不合格
七年级
a
20
24
8
八年级
29
13
13
5
九年级
24
b
14
7
根据以上信息解决下列问题：
（1）在统计表中，a的值为 ， b的值为；
（2）在扇形统计图中，八年级所对应的扇形圆心角为度；
（3）若该校三个年级共有2000名学生参加考试，试估计该校学生体育成绩不合格的人数．
相关试题
