搜索
【题目】如图，已知△ABC的三个顶点的坐标分别为：A（﹣2，3）、B（﹣6，0）、C（﹣1，0）．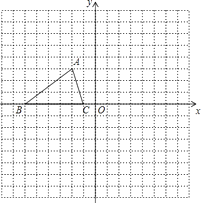 
（1）将△ABC沿y轴翻折，画出翻折后的△A1B1C1 ， 点A的对应点A1的坐标是
（2）△ABC关于x轴对称的图形△A2B2C2 ， 直接写出点A2的坐标
（3）若△DBC与△ABC全等（点D与点A重合除外），请直接写出满足条件点D的坐标．
参考答案：
【答案】
（1）（2，3）
（2）（﹣3，﹣3）
（3）解：如图所示：D（﹣2，﹣3）或（﹣5，3）或（﹣5，﹣3）．
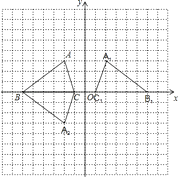
【解析】解：（1）翻折后点A的对应点的坐标是：（2，3）；
所以答案是：（2，3）；（2）如图所示：△A1B1C1 ， 即为所求，A1（﹣2，﹣3）；
【考点精析】解答此题的关键在于理解作轴对称图形的相关知识，掌握画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
-
科目： 来源： 题型：
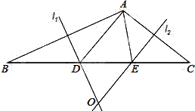
查看答案和解析>>【题目】如图，在△ABC中，AB边的垂直平分线
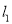交BC于D，AC边的垂直平分线
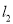交BC于E， 
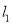与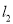
相交于点O，△ADE的周长为6cm．（1）求BC的长；
（2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AC=BC，∠ACB=90°，点D、E在AB上，将△ACD、△BCE分别沿CD、CE翻折，点A、B分别落在点A′、B′的位置，再将△A′CD、△B′CE分别沿A′C、B′C翻折，点D与点E恰好重合于点O，则∠A′OB′的度数是_________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线经过坐标原点O，点A（6，﹣6
），且以y轴为对称轴．
（1）求抛物线的解析式；
（2）如图2，过点B（0，﹣ ）作x轴的平行线l，点C在直线l上，点D在y轴左侧的抛物线上，连接DB，以点D为圆心，以DB为半径画圆，⊙D与x轴相交于点M，N（点M在点N的左侧），连接CN，当MN=CN时，求锐角∠MNC的度数；
（3）如图3，在（2）的条件下，平移直线CN经过点A，与抛物线相交于另一点E，过点A作x轴的平行线m，过点（﹣3，0）作y轴的平行线n，直线m与直线n相交于点S，点R在直线n上，点P在EA的延长线上，连接SP，以SP为边向上作等边△SPQ，连接RQ，PR，若∠QRS=60°，线段PR的中点K恰好落在抛物线上，求Q点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：
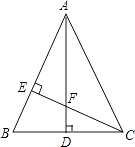
（1）△AEF≌△CEB；
（2）AF=2CD． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为48和36，求△EDF的面积________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABF≌△CDE.
（1）若∠B＝30°，∠DCF＝40°，求∠EFC的度数；
（2）若BD=10，EF=2，求BF的长.
相关试题
