搜索
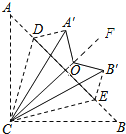
【题目】如图，在△ABC中，AC=BC，∠ACB=90°，点D、E在AB上，将△ACD、△BCE分别沿CD、CE翻折，点A、B分别落在点A′、B′的位置，再将△A′CD、△B′CE分别沿A′C、B′C翻折，点D与点E恰好重合于点O，则∠A′OB′的度数是_________．
参考答案：
【答案】120°
【解析】如图所示：延长CO到F，
∵AC=BC，∠ACB=90°，
∴∠A=∠B=45°，
由翻折的性质可知：∠A′CF=
∠ACF，∠B′CF=∠BCF，
∠CA′O=∠DA′O=∠A=45°，∠OB′C=∠CB′E=∠B=45°，
∴∠A′CB′=∠A′CF+∠B′CF=∠ACB=30°，
∴∠A′OB′=∠A′CB′+∠CA′O+∠OB′C=30°+45°+45°=120°，
故答案为：120°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】暑假期间，某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面．已知这个矩形操场地面的长为100m，宽为80m，图案设计如图所示：操场的四角为小正方形，阴影部分为四个矩形，四个矩形的宽都为小正方形的边长，在实际铺设的过程总，阴影部分铺红色地面砖，其余部分铺灰色地面砖．
（1）如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍，那么操场四角的每个小正方形边长是多少米？
（2）如果灰色地面砖的价格为每平方米30元，红色地面砖的价格为每平方米20元，学校现有15万元资金，问这些资金是否能购买所需的全部地面砖？如果能购买所学的全部地面砖，则剩余资金是多少元？如果不能购买所需的全部地面砖，教育局还应该至少给学校解决多少资金？ -
科目： 来源： 题型：
查看答案和解析>>【题目】⊙O是△ABC的外接圆，AB是直径，过
的中点P作⊙O的直径PG，与弦BC相交于点D，连接AG、CP、PB．
（1）如图1，求证：AG=CP；
（2）如图2，过点P作AB的垂线，垂足为点H，连接DH，求证：DH∥AG；
（3）如图3，连接PA，延长HD分别与PA、PC相交于点K、F，已知FK=2，△ODH的面积为2
，求AC的长． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB边的垂直平分线
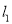交BC于D，AC边的垂直平分线
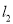交BC于E， 
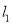与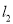
相交于点O，△ADE的周长为6cm．（1）求BC的长；
（2）分别连结OA、OB、OC，若△OBC的周长为16cm，求OA的长；
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，抛物线经过坐标原点O，点A（6，﹣6
），且以y轴为对称轴．
（1）求抛物线的解析式；
（2）如图2，过点B（0，﹣ ）作x轴的平行线l，点C在直线l上，点D在y轴左侧的抛物线上，连接DB，以点D为圆心，以DB为半径画圆，⊙D与x轴相交于点M，N（点M在点N的左侧），连接CN，当MN=CN时，求锐角∠MNC的度数；
（3）如图3，在（2）的条件下，平移直线CN经过点A，与抛物线相交于另一点E，过点A作x轴的平行线m，过点（﹣3，0）作y轴的平行线n，直线m与直线n相交于点S，点R在直线n上，点P在EA的延长线上，连接SP，以SP为边向上作等边△SPQ，连接RQ，PR，若∠QRS=60°，线段PR的中点K恰好落在抛物线上，求Q点坐标．
-
科目： 来源： 题型：
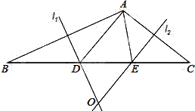
查看答案和解析>>【题目】如图，已知△ABC的三个顶点的坐标分别为：A（﹣2，3）、B（﹣6，0）、C（﹣1，0）．
（1）将△ABC沿y轴翻折，画出翻折后的△A1B1C1 ， 点A的对应点A1的坐标是
（2）△ABC关于x轴对称的图形△A2B2C2 ， 直接写出点A2的坐标
（3）若△DBC与△ABC全等（点D与点A重合除外），请直接写出满足条件点D的坐标． -
科目： 来源： 题型：
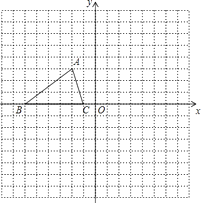
查看答案和解析>>【题目】如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：
（1）△AEF≌△CEB；
（2）AF=2CD．
相关试题
