【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)

参考答案:
【答案】①②
【解析】∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5,
在Rt△ABH中,∠AHB=90∠ABH=67.5,
∵∠AGH=90,
∴∠DAE=∠ABH=22.5,
在△ADE和△CDE中, 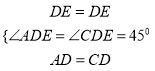 ,
,
∴△ADE≌△CDE,
∴∠DAE=∠DCE=22.5,
∴∠ABH=∠DCF,
在Rt△ABH和Rt△DCF中, 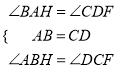 ,
,
∴Rt△ABH≌Rt△DCF,
∴AH=DF,∠CFD=∠AHB=67.5,
∵∠CFD=∠EAF+∠AEF,
∴67.5=22.5+∠AEF,
∴∠AEF=45,故①②正确;
如图,连接HE,
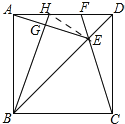
∵BH是AE垂直平分线,
∴AG=EG
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5,
∴∠DHE=45,
∵∠ADE=45,
∴∠DEH=90,∠DHE=∠HDE=45,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故③错误,
∴正确的是①②.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算结果正确的是( )
A. a4﹒a2=a8 B. (a5)2=a7 C. (a-b)2=a2-b2 D. (ab)2=a2b2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(k﹣1)x2﹣2x+1=0有两个不相等的实数根,则k的取值范围是( )
A. k<﹣2 B. k<2 C. k>2 D. k<2且k≠1
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的集合里.
-5,
 ,0,-3.14,
,0,-3.14, 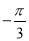 ,
, 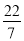 ,2014,+1.99,-(-6),-2.101001000….
,2014,+1.99,-(-6),-2.101001000….(1)正数集合:{________________________…};
(2)负数集合:{_______________________________…};
(3)非负整数集合:{________________________…};
(4)负分数集合:{_______________________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )
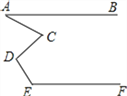
A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
相关试题

