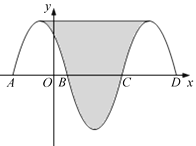
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
参考答案:
【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
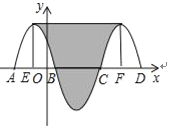
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(21x4y3-35x3y2+7x2y2)÷(-7x2y).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题情境:如图1,在正方形ABCD中,E、F、G、H分别为AB,BC,CD,DA边上的动点,连接EG,HF相交于点O,且∠HOE=∠ADC.试探究:EG与FH的数量关系,并说明理由.
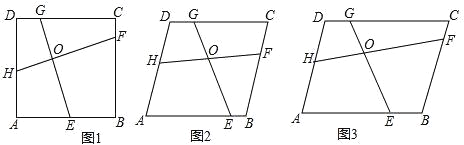
(2)拓展延伸:如图2,在菱形ABCD中,E、F、G、H分别为AB,BC,CD,DA边上的动点,连接EG,HF相交于点O,且∠HOE=∠ADC,试探究:(1)中EG与FH的数量关系还成立吗?并说明理由.
(3)反思提升:若将(2)中的菱形ABCD改为平行四边形ABCD(如图3),AB=a,AD=b,其他条件不变,则
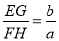 的猜想正确吗?请说明理由.
的猜想正确吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC。

(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合)。问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2-4=0,求代数式x (x+1)2- x(x2+ x)- x-7的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a+2b=5ab B. a3a2=a6 C. a3÷a3=1 D. (3a)2=3a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地一天早晨的气温是-7 ℃,中午气温上升了11 ℃,下午又下降了9 ℃,晚上又下降了5 ℃,则晚上的气温为________ ℃.
相关试题

