【题目】从﹣3、﹣1、 ![]() 、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为 .
、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为 .
参考答案:
【答案】![]()
【解析】解:当a=﹣3,则y=﹣x﹣3,此时图象与x轴交点为:(﹣3,0),与y轴交点为:(0,﹣3),
故一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为4.5,不合题意;
当a=3,则y=﹣x+3,此时图象与x轴交点为:(3,0),与y轴交点为:(0,3),
故一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为4.5,不合题意;
当a=﹣1、 ![]() 、1时,一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为:
、1时,一次函数y=﹣x+a的图象与坐标轴围成三角形的面积为: ![]() ,
, ![]() ,符合题意,
,符合题意,
故关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为: ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了概率公式的相关知识点,需要掌握一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,求证:DECD=DFBE
(2)D为BC中点如图2,连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
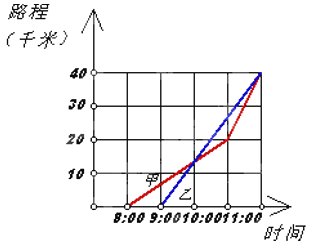
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到十点为止,哪个人的速度快?
(4)两人最终在几点钟相遇?
(5)你能将图象中得到信息,编个故事吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.
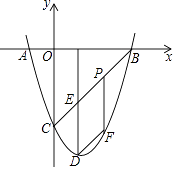
(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距米.
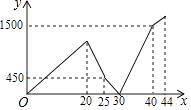
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.4的平方根是2
B.点(﹣3,﹣2)关于x轴的对称点是(﹣3,2)
C. 是无理数
是无理数
D.无理数就是无限小数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形ABCD中,F是CD边上一点(不和C,D重合),过点D做DG⊥BF交BF延长线于点G.连接AG,交BD于点E,连接EF,交CD于点M.若DG=6,AG=7
 ,则EF的长为 .
,则EF的长为 . 
相关试题

