【题目】如图,抛物线y=x2+bx+c与x轴相交于A、B两点,点B的坐标为(3,0),与y轴相交于点C(0,﹣3),顶点为D.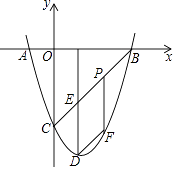
(1)求出抛物线y=x2+bx+c的表达式;
(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①当m为何值时,四边形PEDF为平行四边形.
②设四边形OBFC的面积为S,求S的最大值.
参考答案:
【答案】
(1)解:∵抛物线过B、C两点,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线表达式为y=x2﹣2x﹣3
(2)解:①∵B(3,0),C(0,﹣3),
∴直线BC解析式为y=x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4),
∴E(1,﹣2),
∴DE=﹣2﹣(﹣4)=2,
∵PF∥DE,且P(m,m﹣3),
∴F(m,m2﹣2m﹣3),
∵点P为线段BC上的一个动点,
∴PF=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,
当四边形PEDF为平行四边形时,则有PF=DE=2,
即﹣m2+3m=2,解得m=1(舍去)或m=2,
∴当m的值为2时,四边形PEDF为平行四边形;
②由①可知PF=﹣m2+3m,
∴S△FBC= ![]() PFOB=
PFOB= ![]() ×3(﹣m2+3m)=﹣
×3(﹣m2+3m)=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∵S△OBC= ![]() OBOC=
OBOC= ![]() ×3×3=
×3×3= ![]() ,
,
∴S=S△FBC+S△OBC=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() +
+ ![]() =﹣
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴当m= ![]() 时,S有最大值
时,S有最大值 ![]()
【解析】(1)由B、C两点的坐标,利用待定系数法可求得抛物线的表达式;(2)①可求得直线BC的解析式,则可表示出P、F的坐标,从而可表示出PF和DE的长,由平行四边形的性质可知PF=DE,则可得到关于m的方程,可求得m的值;②用m可表示出PF的长,则可表示出△BCF的面积,从而可表示出四边形OBFC的面积,利用二次函数的性质可求得其最大值.
-
科目: 来源: 题型:
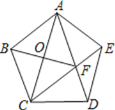
查看答案和解析>>【题目】如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,求证:DECD=DFBE
(2)D为BC中点如图2,连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答:
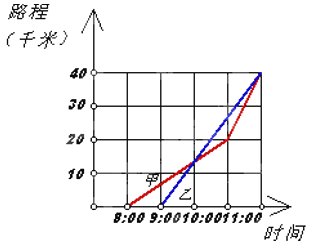
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到十点为止,哪个人的速度快?
(4)两人最终在几点钟相遇?
(5)你能将图象中得到信息,编个故事吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3、﹣1、
 、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为 .
、1、3这五个数中,随机抽取一个数,记为a,则关于x的一次函数y=﹣x+a的图象与坐标轴围成三角形的面积不超过4的概率为 . -
科目: 来源: 题型:
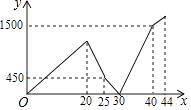
查看答案和解析>>【题目】小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.4的平方根是2
B.点(﹣3,﹣2)关于x轴的对称点是(﹣3,2)
C. 是无理数
是无理数
D.无理数就是无限小数
相关试题

