【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),点D在△ABC内,且BD=BC,∠DBC=60°.
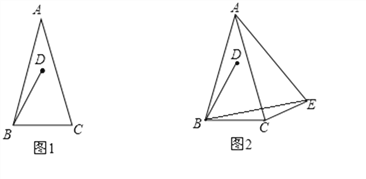
(1)如图1, 连接AD,直接写出∠ABD的度数(用含α的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.
参考答案:
【答案】(1)30°- ![]() ;(2) △ABE是等边三角形,证明见解析;(3)30°.
;(2) △ABE是等边三角形,证明见解析;(3)30°.
【解析】试题分析:(1)求出∠ABC的度数,即可求出答案;
(2)连接AD,CD,ED,根据旋转性质得出BC=BD,∠DBC=60°,求出∠ABD=∠EBC=30°-![]() α,且△BCD为等边三角形,证△ABD≌△ACD,推出∠BAD=∠CAD=
α,且△BCD为等边三角形,证△ABD≌△ACD,推出∠BAD=∠CAD=![]() ∠BAC=
∠BAC=![]() α,求出∠BEC=
α,求出∠BEC=![]() α=∠BAD,证△ABD≌△EBC,推出AB=BE即可;
α=∠BAD,证△ABD≌△EBC,推出AB=BE即可;
(3)求出∠DCE=90°,△DEC为等腰直角三角形,推出DC=CE=BC,求出∠EBC=15°,得出方程30°-![]() α=15°,求出即可.
α=15°,求出即可.
试题解析:(1)(1)∵AB=AC,∠A=α,
∴∠ABC=∠ACB=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() α,
α,
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,
即∠ABD=30°-![]() α;
α;
(2)△ABE是等边三角形,理由如下:
连接AD,CD,
∵∠ABE=60°, ∠ABD=30°- ![]() ,
,
∴∠DBE=30°+ ![]() ,
,
又∵∠DBC=60°,
∴∠CBE=30°- ![]() =∠ABD,
=∠ABD,
∵∠DBC=60°,BD=BC,
∴△BDC是等边三角形,
∴BD=CD,
在△ABD和△ACD中,AB=AC,BD=CD,AD=AD,
∴△ABD≌△ACD,
∴∠BAD=∠CAD= ![]() ,
,
在△BCE中,∠BCE=150°,∠CBE=30°- ![]() ,
,
∴∠BEC= ![]() =∠BAD,
=∠BAD,
在△ABD和△CBE中, ∠BEC=∠BAD, ∠CBE=∠ABD,AB=AC,
∴△ABD≌△CBE,
∴AB=BE,
又∵∠ABE=60°,
∴△ABE是等边三角形;
(3)由(2)知△BDC是等边三角形,
∴∠BCD=60°,
∵∠BCE=150°,
∴∠DCE=90°,
∵∠DEC=45°,
∴△DCE是等腰直角三角形,
∴CD=CE=BC,在△BCE中, ∠BCE=150°,
∴∠CBE=30°- ![]() =15°,
=15°,
∴a=30°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了估计一个鱼塘里鱼的数量,第一次打捞上来20条,做上记号放入水中,第二次打捞上来25条,其中4条有记号,鱼塘大约有鱼__________条.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系
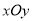 中的点
中的点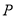 ,给出如下定义:记点
,给出如下定义:记点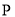 到
到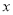 轴的距离为
轴的距离为 ,到
,到 轴的距离为
轴的距离为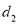 若
若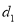 ≤
≤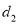 ,则称
,则称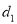 为点
为点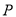 的“引力值”;若
的“引力值”;若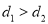 ,则称
,则称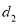 为点
为点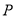 的“引力值”.特别地,若点
的“引力值”.特别地,若点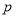 在坐标轴上,则点
在坐标轴上,则点 的“引力值”为0.
的“引力值”为0.例如,点P(-2,3)到
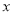 轴的距离为3 ,到
轴的距离为3 ,到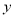 轴的距离为2 ,因为2<3,所以点
轴的距离为2 ,因为2<3,所以点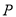 的“引力值”为2.
的“引力值”为2.(1)①点
 的“引力值”为 ;②若点
的“引力值”为 ;②若点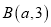 的“引力值”为2,则
的“引力值”为2,则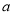 的值为 ;
的值为 ;(2)若点C在直线
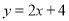 上,且点C的:“引力值”为2,求点C的坐标;
上,且点C的:“引力值”为2,求点C的坐标;(3)已知点M是以D(3,4)为圆心,半径为2的圆上的一个动点,那么点M的“引力值”
 的取值范围是
的取值范围是 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是假命题的是( )
A.对顶角相等B.同旁内角互补C.两点确定一条直线D.垂线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E,∠ABC的平分线BF交CD于点F,过点A作AH⊥CD于H,当EDC=30
 ,CF=
,CF= ,则DH=______.
,则DH=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40kg,了解到这些蔬菜的种植成本共42元,还了解到如下信息:

(1)请问采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
相关试题

