【题目】如图,长方形ABCD中,AB=2,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为__.

参考答案:
【答案】2或![]()
【解析】
当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=![]() ,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=2,可计算出CB′=
,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=2,可计算出CB′=![]() -2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
-2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
解:当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=2,BC=4,
∴![]() ,
,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=2,
∴CB′=![]() ,
,
设BE=x,则EB′=x,CE=4-x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴![]()
即:![]() ,
,
解得:![]() ;
;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,
∴BE=AB=2.
故答案为:2或![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由四个全等的直角三角形拼成的大正方形的面积为84,中间小正方形的面积为24,若直角三角形较长直角边为
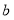 ,较短直角边为
,较短直角边为 ,则
,则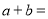 __.
__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(m,6),B(n,1)在反比例函数
 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 已知反比例函数
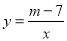 的图象的一支位于第一象限.
的图象的一支位于第一象限.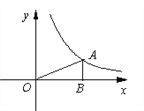
(1)该函数图象的另一分支位于第_____象限,m的取值范围是____________;
(2)已知点A在反比例函数图象上,AB⊥x轴于点B,△AOB的面积为3,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=ax2+bx+c. 当x=1时,y=0;当x=2时,y=4;当x=3时,y=10.
(1)求a、b、c的值;
(2)求x=4时,y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下两则材料,解决后续问题:
材料一:我们可以将任意三位数记为
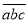 (其中a,b,c,分别表示该数的百位数字、十位数字和个位数字,且a≠0,显然
(其中a,b,c,分别表示该数的百位数字、十位数字和个位数字,且a≠0,显然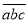 =100a+10b+c.
=100a+10b+c.材料二:若一个三位数的三个数字均不为0且三个数字互不相等,则称之为原始数,比如123就是一个原始数.将原始数的三个数位数字交换顺序,可产生出5个新的原始数,比如由123可以产生出132、213、231、312、321这5个新原始数.将这6个数相加,得到的和1332称为由原始数123生成的终止数.
问题:(1)求原始数247生成的终止数;
(2)试说明所有的原始数生成的终止数都能被222整除;
(3)若一个原始数生成的终止数为
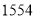 ,求满足条件的所有原始数.
,求满足条件的所有原始数. -
科目: 来源: 题型:
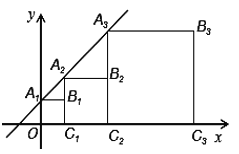
查看答案和解析>>【题目】如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则A4的坐标是____,通过你对A1、A2、A3…坐标的研究发现,得出An的坐标是_____.
相关试题

