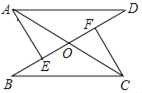
【题目】如图,已知AC、BD相交于点O,AD=BC,AE⊥BD于点E,CF⊥BD于点F,BE=DF.求证:
(1)△ADE≌△CBF;
(2)OA=OC.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由BE=DF,可得BF=DE,则根据“HL”可证Rt△ADE≌Rt△CBF;
(2)由Rt△ADE≌Rt△CBF可得AE=CF,根据“AAS”可证△AOE≌△COF,可得OA=OC.
证明:(1)∵BE=DF
∴BE+EF=DF+EF
∴BF=DE,且AD=BC
∴Rt△ADE≌Rt△CBF(HL)
(2)∵Rt△ADE≌Rt△CBF
∴AE=CF,且∠AEO=∠CFO=90°,∠AOE=∠COF
∴△AOE≌△COF(AAS)
∴OA=OC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,
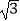 ≈1.73)
≈1.73)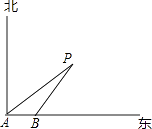
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有________.
①.体育场离小冬家2.5千米 ②.小冬在体育场锻炼了15分钟
③.体育场离早餐店4千米 ④.小冬从早餐店回家的平均速度是3千米/小时
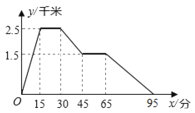
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.

∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线
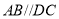 ,点
,点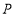 为平面上一点,连接
为平面上一点,连接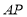 与
与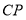 .
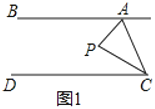
.(1)如图1,点
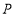 在直线
在直线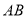 、
、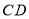 之间,当
之间,当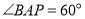 ,
,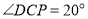 时,求
时,求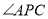 .
.
(2)如图2,点
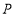 在直线
在直线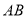 、
、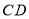 之间
之间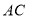 左侧,
左侧,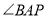 与
与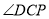 的角平分线相交于点
的角平分线相交于点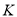 ,写出
,写出 与
与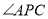 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.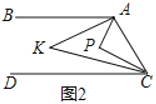
(3)如图3,点
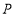 落在
落在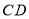 下方,
下方,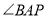 与
与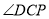 的角平分线相交于点
的角平分线相交于点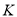 ,
, 与
与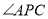 有何数量关系?并说明理由.
有何数量关系?并说明理由.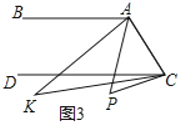
相关试题

