【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1, ![]() ≈1.73)
≈1.73)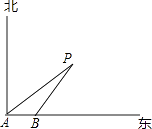
参考答案:
【答案】解:过点P作PC⊥AB于C点,即PC的长为轮船与灯塔的最短距离,根据题意,得
AB=18× ![]() =6,∠PAB=90°﹣60°=30°,∠PBC=90°﹣45°=45°,∠PCB=90°,
=6,∠PAB=90°﹣60°=30°,∠PBC=90°﹣45°=45°,∠PCB=90°,
∴PC=BC,
在Rt△PAC中,tan30°= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得PC=3 ![]() +3≈8.2(海里),
+3≈8.2(海里),
∴轮船与灯塔的最短距离约为8.2海里.
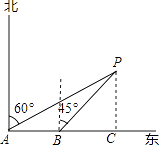
【解析】根据题意,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,得到AB![]() =6,∠PAB=30°,∠PBC=45°,∠PCB=90°,所以PC=BC,在Rt△PAC中,根据三角函数值求出tan3
=6,∠PAB=30°,∠PBC=45°,∠PCB=90°,所以PC=BC,在Rt△PAC中,根据三角函数值求出tan3![]() 0°,
0°,![]() 解得PC≈8.2(海里),所以轮船与灯塔的最短距离约为8.2海里.
解得PC≈8.2(海里),所以轮船与灯塔的最短距离约为8.2海里.
【考点精析】掌握关于方向角问题是解答本题的根本,需要知道指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
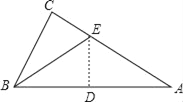
A. 2
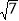 B.
B. 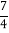 C.
C.  D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是 .
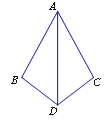
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论. -
科目: 来源: 题型:
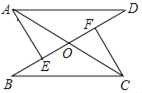
查看答案和解析>>【题目】如图,已知AC、BD相交于点O,AD=BC,AE⊥BD于点E,CF⊥BD于点F,BE=DF.求证:
(1)△ADE≌△CBF;
(2)OA=OC.
相关试题

