【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
参考答案:
【答案】
(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中

∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
(2)解:四边形ADCF是菱形,
证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,
∴AD= ![]() BC=DC,
BC=DC,
∴平行四边形ADCF是菱形.
【解析】(1)由平行线的性质可知:AF∥BC,得到∠AFE=∠DBE,又E是AD的中点,AD是BC边上的中线,得到AE=DE,BD=CD,所以△AFE≌△DBE(AAS),AF=BD,即AF=DC;(2)AF∥BC,AF=DC,根据平行四边形的定义得到四边形ADCF是平行四边形,又AC⊥AB,AD是斜边BC的中线,得到AD= ![]() BC=DC,根据菱形的定义得到平行四边形ADCF是菱形.
BC=DC,根据菱形的定义得到平行四边形ADCF是菱形.
-
科目: 来源: 题型:
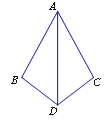
查看答案和解析>>【题目】如图,在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班“2016年联欢会”中,有一个摸奖游戏:有4张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,2张是哭脸,现将4张纸牌洗匀后背面朝上摆放到桌上,然后让同学去翻纸牌.
(1)现在小芳和小霞分别有一次翻牌机会,若正面是笑脸,则小芳获奖;若正面是哭脸,则小霞获奖,她们获奖的机会相同吗?判断并说明理由.
(2)如果小芳、小明都有翻两张牌的机会.翻牌规则:小芳先翻一张,放回后再翻一张;小明同时翻开两张纸牌.他们翻开的两张纸牌中只要出现笑脸就获奖.请问他们获奖的机会相等吗?判断并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,
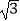 ≈1.73)
≈1.73)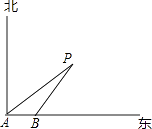
-
科目: 来源: 题型:
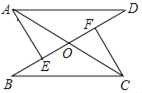
查看答案和解析>>【题目】如图,已知AC、BD相交于点O,AD=BC,AE⊥BD于点E,CF⊥BD于点F,BE=DF.求证:
(1)△ADE≌△CBF;
(2)OA=OC.
-
科目: 来源: 题型:
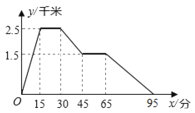
查看答案和解析>>【题目】如图所示:图象中所反映的过程是:小冬从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x轴表示时间,y轴表示小冬离家的距离.根据图象提供的信息,下列说法正确的有________.
①.体育场离小冬家2.5千米 ②.小冬在体育场锻炼了15分钟
③.体育场离早餐店4千米 ④.小冬从早餐店回家的平均速度是3千米/小时
相关试题

