【题目】如图,矩形ABCD中,AB=5,BD=13,Rt△EFG的直角边GE在CB的延长线上,E点与矩的B点重,∠FGE=90°,FG=3.将矩形ABCD固定,把Rt△EFG沿着射线BC方向运动,当点F恰好经过BD时,将△EFG绕点F逆时针旋转α°(0°<α°<90°),记旋转中的△EFG为△E′F′G′,在旋转过程中,设直线E′G′与直线BC交于N,与直线BD交于M点,当△BMN为以MN为底边的等腰三角形时,FM的长为 . 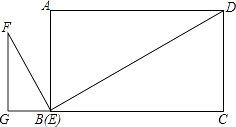
参考答案:
【答案】3 ![]()
【解析】解:如图,作BR平分∠DBC交CD于R,RT⊥BD垂足为T,
∵四边形ABCD是矩形,
∴AB=CD=5,∠C=90°,
∵BD=13,
∴BC= ![]() =
= ![]() =12,
=12,
在△BRT和△BRC中, ,
,
∴△BRT≌△BRC,
∴BT=BC=12,TD=1,设RT=RC=x,
在RT△RTD中,∵TD2+RT2=RD2 ,
∴x2+12=(5﹣X)2 ,
∴x= ![]() ,
,
∴BR= ![]() =
= ![]() =
= ![]() ,
,
∵BN=BM,
∴∠BMN=∠BNM,
∵∠DBC=∠BMN+∠BNM,∠RBD=∠RBC,
∴∠TBR=∠FMG′,
∵∠RTB=∠FG′M=90°,
∴△BTR∽△MG′F,
∴ ![]() ,
,
∴ ![]() ,
,
∴FM=3 ![]() .
.
【考点精析】关于本题考查的旋转的性质,需要了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能得出正确答案.
-
科目: 来源: 题型:
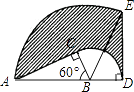
查看答案和解析>>【题目】如图,△ABC中,∠C是直角,AB=6cm,∠ABC=60°,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的D处,则AC边扫过的图形众人阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣1,0,1,3,4,这五个数中任选一个数记为a,则使双曲线y=
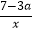 在第一、三象限且不等式组
在第一、三象限且不等式组 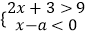 无解的概率是 .
无解的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两人均从400米的环形跑道的A处出发,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若两人同时出发,背向而行,则经过 秒钟两人第一次相遇;若两人同时出发,同向而行,则经过 秒钟乙第一次追上甲.
(2)若两人同向而行,乙在甲出发10秒钟后去追甲,经过多少时间乙第二次追上甲.
(3)若让甲先跑10秒钟后乙开始跑,在乙用时不超过100秒的情况下,乙跑多少秒钟时,两人相距40米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的两条中线AD、BE交于点F,连接CF,若△ABC的面积为24,则△ABF的面积为( )

A. 10 B. 8 C. 6 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)2x(x+1)﹣(x+2)(x﹣2)+(x﹣1)2
(2)(x﹣1﹣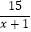 )
) 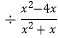 .
. -
科目: 来源: 题型:
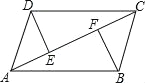
查看答案和解析>>【题目】已知DE⊥AC,BF⊥AC,垂足分别是E、F,AE=CF,DC∥AB,
(1)试证明:DE=BF;
(2)连接DF、BE,猜想DF与BE的关系?
相关试题

