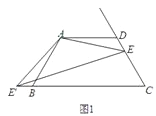
【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
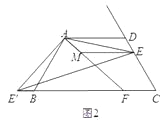
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
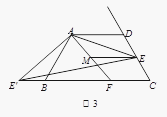
(3)如图3,在(2)的条件下,如果CE=2,AE=![]() ,求ME的长.
,求ME的长.
参考答案:
【答案】(1)∠AEE'=30°;
(2)当点E在线段CD上时,![]() ;
;
当点E在CD的延长线上时,
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
(3)![]() .
.
【解析】
试题(1)根据旋转地的性质易得到△ADE≌△ABE/,∠EAE/=120°,所以∠AEE/=30°.
由于点E是射线CD上一动点,其位置不确定,故应分情况讨论:一是当点E在线段CD上时:此时易得![]() ;二是点E在CD的延长线上时,仍需考虑多种情况,可以知道,当∠EAD=300时,AE旋转后的直线与BC平行,当∠EAD=900时,AE旋转后的直线与AB共线,而∠EAD不可能为1200,所以应再次细分为三种情况:即当
;二是点E在CD的延长线上时,仍需考虑多种情况,可以知道,当∠EAD=300时,AE旋转后的直线与BC平行,当∠EAD=900时,AE旋转后的直线与AB共线,而∠EAD不可能为1200,所以应再次细分为三种情况:即当![]() 时;当
时;当![]() 时;当
时;当![]() 时.
时.
(3)如图,作![]() 于点G, 作
于点G, 作![]() 于点H.易知四边形AGHD是矩形和两个全等的直角三角形
于点H.易知四边形AGHD是矩形和两个全等的直角三角形![]() ;∴点
;∴点![]() 、B、C在一条直线上.继续作
、B、C在一条直线上.继续作![]() 于Q.
于Q.![]() 于点P. 多次利用勾股定理可得
于点P. 多次利用勾股定理可得![]() ,
,![]() ,
,![]() ;继而证明Rt△AG E'∽Rt△FA E',根据相似三角形性质可求解.
;继而证明Rt△AG E'∽Rt△FA E',根据相似三角形性质可求解.
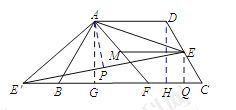
试题解析:
解:(1) 30°.
当点E在线段CD上时,![]() ;
;
当点E在CD的延长线上,
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .
.
(3)作![]() 于点G, 作
于点G, 作![]() 于点H.
于点H.
由AD∥BC,AD=AB=CD,∠BAD=120°,得∠ABC=∠DCB=60°,
易知四边形AGHD是矩形和两个全等的直角三角形![]() .则GH="AD" , BG=CH.
.则GH="AD" , BG=CH.
∵![]() ,
,
∴点![]() 、B、C在一条直线上.设AD=AB=CD=x,则GH=x,BG=CH=
、B、C在一条直线上.设AD=AB=CD=x,则GH=x,BG=CH=![]() ,.
,.
作![]() 于Q.在Rt△EQC中,CE="2,"
于Q.在Rt△EQC中,CE="2,"![]() ,
,
∴![]() ,
,![]() .
.
∴E'Q=![]() .
.
作![]() 于点P.
于点P.
∵△ADE绕点A顺时针旋转120°后,得到△ABE'.
∴△A EE'是等腰三角形,![]() .
.
∴在Rt△AP E'中,E'P=![]() .
.
∴EE'="2" E'P=![]() .
.
∴在Rt△EQ E'中,E'Q=![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]()
在Rt△E'AF中,![]()
∴Rt△AG E'∽Rt△FA E'.
∴![]()
∴![]() .
.
∴![]() .
.
由(2)知:![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
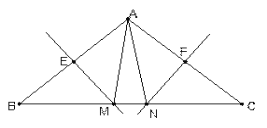
查看答案和解析>>【题目】如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)若BC =10cm,试求△AMN的周长.
(2)在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
-
科目: 来源: 题型:
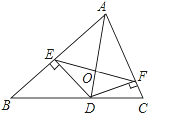
查看答案和解析>>【题目】如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中.AB=AC.∠BAC=90
 .E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
.E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.(l)图中是否存在两个三角形全等?如果存在请写出哪两个三角形全等,并且证明;如果不存在,请说明理由;
(2)若∠CBE=30
 ,求∠ADC的度数.
,求∠ADC的度数.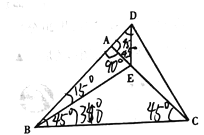
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=
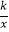 (x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.
(x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.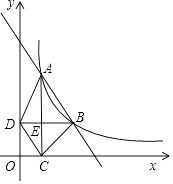
(1)若△ABD的面积为3,求k的值和直线AB的解析式;
(2)求证: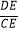 =
=  ;
;
(3)若AD∥BC,求点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=
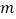 (
(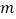 为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.(1)如图,当点C恰好在线段AB中点时,则PQ=_______(用含
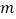 的代数式表示);
的代数式表示);(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ-2PQ与1的大小关系,并说明理由。
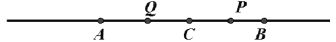
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD、DE、BE,则下列结论:①∠ECA=165°,②BE=BC;③AD=BE;④CD=BD.其中正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
相关试题

