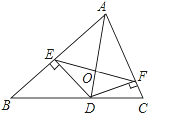
【题目】如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.
参考答案:
【答案】(1)详见解析;(2) 垂直,理由详见解析;(3)四边形AEDF的面积为4﹣![]() .
.
【解析】
(1)由角平分线的性质直接可得到DE=DF;
(2)可证明△AED≌△AFD,可知AE=AF,利用线段垂直平分线的判定可证明AD是EF的垂直平分线,可证得结论;
(3)设△CDF的面积为x,则可分别表示出△BED、△ADE的面积,利用三角形的面积可分别表示出DE和DF,根据DE=DF可得到关于x的方程,可求得x的值,进一步可求得四边形AEDF的面积.
(1)∵AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,∴DE=DF(角平分线的性质);
(2)垂直.理由如下:
∵AD是△ABC的角平分线,∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,∴∠AED=∠AFD=90°.
在Rt△AED和Rt△AFD中,∵
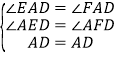 ,∴Rt△AED≌Rt△AFD(AAS),∴AE=AF,∴点A在线段EF的垂直平分线上,同理点D也在线段EF的垂直平分线上,∴AD⊥EF;
,∴Rt△AED≌Rt△AFD(AAS),∴AE=AF,∴点A在线段EF的垂直平分线上,同理点D也在线段EF的垂直平分线上,∴AD⊥EF;
(3)设S△CDF=x,则S△BDE=2x.
∵S△ACD=1,且△AED≌△AFD,∴S△AED=S△AFD=1﹣x,∴S△ABD=S△BDE+S△AED=2x+1﹣x=x+1,又S△ABD![]() ABDE,S△ACD
ABDE,S△ACD![]() ACDF,且AB=c,AC=b,∴
ACDF,且AB=c,AC=b,∴![]() cDE=x+1,
cDE=x+1,![]() bDF=1,∴DE
bDF=1,∴DE![]() ,DF
,DF![]() ,又由(1)可知DE=DF,∴
,又由(1)可知DE=DF,∴![]() ,解得:x
,解得:x![]() 1.
1.
∵△AED≌△AFD,∴S△AED=S△AFD=S△ACD﹣S△CDF=1﹣x,∴S四边形AEDF=2S△AED=2(1﹣x)=2[1﹣(![]() 1)]=4
1)]=4![]() ,即四边形AEDF的面积为4
,即四边形AEDF的面积为4![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、O、B在一条直线上,将射线OC绕O点顺时针方向旋转90°后,得到射线OD,在旋转过程中,射线OC始终在直线AB上方,且OE平分∠AOD.约定,无论∠AOD大小如何,OE都看作是由OA、OD两边形成的最小角的平分线.
(1)如图,当∠AOC=30°时,∠BOD=_________°;
(2)若射线OF平分∠BOC,求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

-
科目: 来源: 题型:
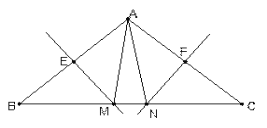
查看答案和解析>>【题目】如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)若BC =10cm,试求△AMN的周长.
(2)在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中.AB=AC.∠BAC=90
 .E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
.E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.(l)图中是否存在两个三角形全等?如果存在请写出哪两个三角形全等,并且证明;如果不存在,请说明理由;
(2)若∠CBE=30
 ,求∠ADC的度数.
,求∠ADC的度数.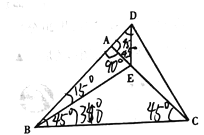
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
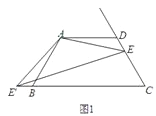
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
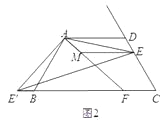
(3)如图3,在(2)的条件下,如果CE=2,AE=
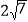 ,求ME的长.
,求ME的长.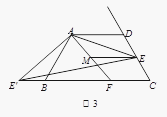
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=
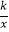 (x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.
(x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.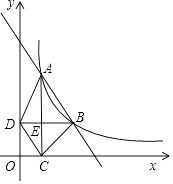
(1)若△ABD的面积为3,求k的值和直线AB的解析式;
(2)求证: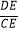 =
=  ;
;
(3)若AD∥BC,求点B的坐标.
相关试题

