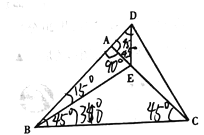
【题目】如图,在△ABC中.AB=AC.∠BAC=90![]() .E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
.E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
(l)图中是否存在两个三角形全等?如果存在请写出哪两个三角形全等,并且证明;如果不存在,请说明理由;
(2)若∠CBE=30![]() ,求∠ADC的度数.
,求∠ADC的度数.
参考答案:
【答案】(1)存在两个三角形全等,△ABE≌△ACD,理由见解析;(2)75![]()
【解析】试题分析:(1)根据AE=AD,AB=AC,∠DAC=∠BAE=90°,根据SAS即可推出△ABE≌△ACD;
(2)由(1)△ABD≌△ACE,可得∠ABE=∠ACD,由已知可得∠ABE=15°,再根据三角形的外角即可得∠ADC的度数.
试题解析:(1)存在两个三角形全等 ,
它们是△ABE≌△ACD;
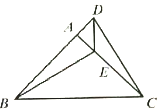
在△ABE和△ACD中,
∵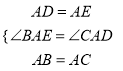 ,
,
∴△ABE≌△ACD;
(2)∵AB=AC , ∠BAC=90![]() ,
,
∴∠ABC=45![]() ,
,
∵△ABE≌△ACD,
∴∠ABE=∠ACD,
∵∠ABE=∠ABC-∠CBE=45![]() -30
-30![]() =15
=15![]() ,
,
∵∠BAC=∠ADC+∠ACD,
∴∠ADC=∠BAC-∠ACD=90![]() -15
-15![]() =75
=75![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

-
科目: 来源: 题型:
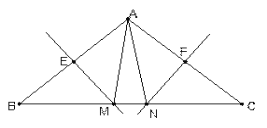
查看答案和解析>>【题目】如图,在△ABC中,ME和NF分别垂直平分AB和AC.
(1)若BC =10cm,试求△AMN的周长.
(2)在△ABC中,AB = AC,∠BAC = 100°,求∠MAN的度数.
(3) 在 (2) 中,若无AB = AC的条件,你还能求出∠MAN的度数吗?若能,请求出;若不能,请说明理由.
-
科目: 来源: 题型:
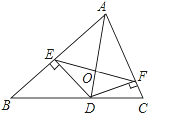
查看答案和解析>>【题目】如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.
-
科目: 来源: 题型:
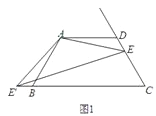
查看答案和解析>>【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
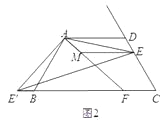
(3)如图3,在(2)的条件下,如果CE=2,AE=
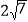 ,求ME的长.
,求ME的长.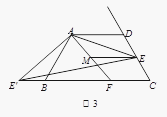
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=
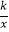 (x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.
(x>0,k是常数)的图象经过A(2,6),B(m,n),其中m>2.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连结AD,DC,CB.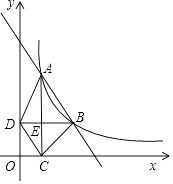
(1)若△ABD的面积为3,求k的值和直线AB的解析式;
(2)求证: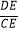 =
=  ;
;
(3)若AD∥BC,求点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=
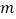 (
(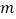 为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.(1)如图,当点C恰好在线段AB中点时,则PQ=_______(用含
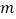 的代数式表示);
的代数式表示);(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ-2PQ与1的大小关系,并说明理由。
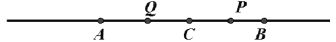
相关试题

