【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于_____.
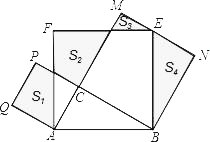
参考答案:
【答案】6
【解析】
过F作AM的垂线交AM于D,通过证明S2=SRt△ABC;S3=SRt△AQF=SRt△ABC;S4=SRt△ABC,进而即可求解.
解:过F作AM的垂线交AM于D,
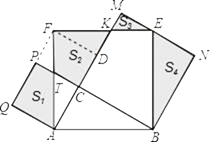
可证明Rt△ADF≌Rt△ABC,Rt△DFK≌Rt△CAT,
所以S2=SRt△ABC.
由Rt△DFK≌Rt△CAT可进一步证得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT,
又可证得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC.
易证Rt△ABC≌Rt△EBN,
∴S4=SRt△ABC,
∴S1﹣S2+S3+S4
=(S1+S3)﹣S2+S4
=SRt△ABC﹣SRt△ABC+SRt△ABC
=6﹣6+6
=6,
故答案是:6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民使用自来水按月收费,标准如下:
①若每户月用水不超过
 ,按
,按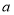 元/
元/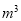 收费;
收费;②若超过
 ,但不超过
,但不超过 ,则超过的部分按
,则超过的部分按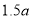 元/
元/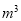 收费,未超过
收费,未超过 部分按①标准收费;
部分按①标准收费;③若超过
 ,超过的部分按
,超过的部分按 元/
元/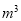 收费,未超过
收费,未超过 部分按②标准收费;
部分按②标准收费;(1)若用水
 ,应交水费______元;(用含
,应交水费______元;(用含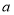 的式子表示)
的式子表示)(2)小明家上个月用水
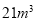 ,交水费
,交水费 元,求
元,求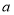 的值;
的值;(3)在(2)的条件下,小明家七、八两个月共交水费
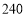 元,七月份用水
元,七月份用水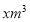 超过
超过 ,但不足
,但不足 ,八月份用水
,八月份用水 超过
超过 ,当
,当 均为整数时,求
均为整数时,求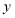 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.

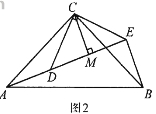
(3)解决问题如图3,在正方形ABCD中,CD=
 .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙二人同时从学校出发,沿同一方向匀速行走,
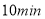 后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了
后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了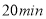 .两人在行走过程中得到如下表所示的信息:
.两人在行走过程中得到如下表所示的信息:离开学校的时间
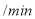
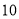
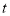
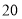
甲离学校的距离
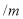
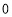
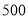
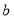
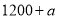
乙离学校的距离
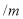
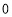
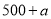
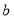
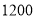
(1)根据题意,甲出发时的速度为_______
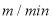 ,乙的速度为______
,乙的速度为______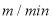 ;
;(2)求表中
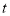 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:
问题:现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形,要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得
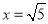 ,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.
,由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长,于是,画出如图②所示的分割线,拼出如图③所示的新正方形.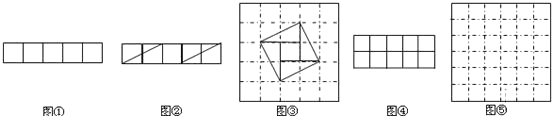
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的正方形,排列形式如图④,请把它们分割后拼接成一个新的正方形,要求:在图④中画出分割线,并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.(说明:直接画出图形,不要求写分析过程.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由边长为1 的正方体搭成的立体图形,第(1)个图形由1个正方体搭成,第(2)个图形由4个正方体搭成,第(3)个图形由10个正方体搭成,以此类推,搭成第(6)个图形所需要的正方体个数是( )
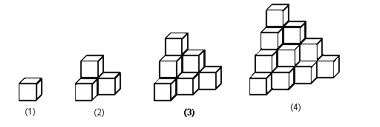
A.84个B.56个C.37个D.36个
相关试题

