【题目】已知AB∥CD.
如图1,你能得出∠A+∠E+∠C=360°吗?
如图2,猜想出∠A.∠C、∠E的关系式并说明理由.
如图3,∠A.∠C、∠E的关系式又是什么?

参考答案:
【答案】图2中,∠A+∠C=∠E;图3中∠A+∠E-∠C=180°。
【解析】
过点E作AB的平行线EF,根据平行公理的推论得出EF∥CD,再根据平行线的性质进行推导,即可得出∠A、∠E、∠C之间的关系.
图1:过E作EF∥AB,如图所示:
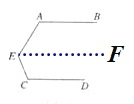
∴∠A+∠AEF=180°(两直线平行,同旁内角互补)
∵AB∥CD(已知)
∴EF∥CD(平行公理的推论)
∴∠C+∠FEC=180°
结论:∠A+∠C+∠AEC=360°;
图2:过E作EF∥AB,如图所示:

∴EF//CD,∠BAE=∠AEF
∴∠FEC=∠DCE
∴∠A+∠C=∠FEC+∠AEF,即∠A+∠C=∠E.
图3:过E作EF∥AB,如图所示:
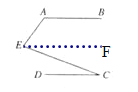
∴EF//CD,∠A+∠AEF=180°,
∴∠C=∠FEC,
∴∠A+∠FEC +∠AEF=180°+∠C, 即∠A+∠E-∠C=180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求CE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进A.B两种商品共160件,其进价和售价如表:
A
B
进价(元/件)
15
35
售价(元/件)
20
45
(1)当A.B两种商品分别购进多少件时,商店计划售完这批商品后能获利1100元;
(2)若商店计划购进A种商品不少于66件,且销售完这批商品后获利多于1260元,请你帮该商店老板预算有几种购货方案?获利最大是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A.
 B. 3 C. 1 D.
B. 3 C. 1 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】讲完“有理数的除法”后,老师在课堂上出了一道计算题:15
 ÷(-8).不一会儿,不少同学算出了答案,老师把班上同学的解题过程归类写到黑板上.
÷(-8).不一会儿,不少同学算出了答案,老师把班上同学的解题过程归类写到黑板上.方法一:原式=
 ×(-
×(- )=-
)=- =-1
=-1 ;
;方法二:原式=(15+
 )×(-
)×(- )=15×(-
)=15×(- )+
)+ ×(-
×(- )=-
)=- =-1
=-1 ;
;方法三:原式=(16-
 )÷(-8)=16÷(-8)-
)÷(-8)=16÷(-8)- ÷(-8)=-2+
÷(-8)=-2+ =-1
=-1 .
.对这三种方法,大家议论纷纷,你认为哪种方法最好?请说出理由,并说说本题对你有何启发.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
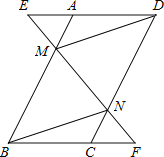
(1)求证:△AEM≌△CFN;
(2)求证:四边形BMDN是平行四边形.
相关试题

