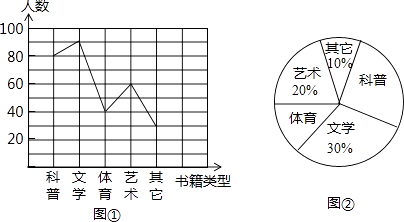
【题目】2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题: 
(1)在这次抽样调查中,一共调查了多少名学生?
(2)请把折线统计图(图1)补充完整;
(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;
(4)如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.
参考答案:
【答案】
(1)解:90÷30%=300(名),
故,一共调查了300名学生;
(2)解:艺术的人数:300×20%=60名,
其它的人数:300×10%=30名;
补全折线图如图
(3)解:体育部分所对应的圆心角的度数为: ![]() ×360°=48°;
×360°=48°;
(4)解:1800× ![]() =480(名).
=480(名).
答:1800名学生中估计最喜爱科普类书籍的学生人数为480.
【解析】(1)用文学的人数除以所占的百分比计算即可得解;(2)根据所占的百分比求出艺术和其它的人数,然后补全折线图即可;(3)用体育所占的百分比乘以360°,计算即可得解;(4)用总人数乘以科普所占的百分比,计算即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
 x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D
x+1与抛物线y=ax2+bx﹣3交于A,B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D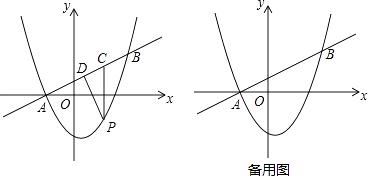
(1)①求抛物线的解析式;②求sin∠ACP的值
(2)设点P的横坐标为m
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成两个三角形,求出当这两个三角形面积之比为9:10时的m值;
③是否存在适合的m值,使△PCD与△PBD相似?若存在,直接写出m值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小王乘公共汽车从甲地到相距40千米的乙地办事,然后乘出租车返回,出租车的平均速度比公共汽车多20千米/时,回来时路上所花时间比去时节省了
 ,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
,设公共汽车的平均速度为x千米/时,则下面列出的方程中正确的是( )
A.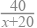 =
=  ×
× 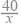
B.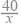 =
=  ×
× 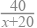
C.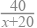 +
+  =
= 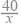
D.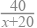 ﹣
﹣  =
= 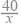
-
科目: 来源: 题型:
查看答案和解析>>【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数1至2018按一定规律排列如下表:
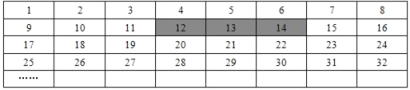
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2018 B. 2019 C. 2040 D. 2049
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并填空:
寻求某些勾股数的规律:
⑴对于任何一组已知的勾股数都扩大相同的正整数倍后,就得到了一组新的勾股数.例如:
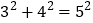 ,我们把它扩大2倍、3倍,就分别得到
,我们把它扩大2倍、3倍,就分别得到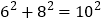 和
和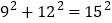 ,……若把它扩大11倍,就得到 ,若把它扩大n倍,就得到 .
,……若把它扩大11倍,就得到 ,若把它扩大n倍,就得到 .⑵对于任意一个大于1的奇数,存在着下列勾股数:
若勾股数为3,4,5,因为,则有
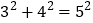 ;
;若勾股数为5,12,13,则有
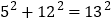 ;
;若勾股数为7,24,25,则有 ;……
若勾股数为m(m为奇数),n, ,则有m2= ,用m来表示n= ;
当m=17时,则n= ,此时勾股数为 .
⑶对于大于4的偶数:
若勾股数为6,8,10,因为
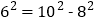 ,则有……请找出这些勾股数之间的关系,并用适当的字母表示出它的规律来,并求当偶数为24的勾股数.
,则有……请找出这些勾股数之间的关系,并用适当的字母表示出它的规律来,并求当偶数为24的勾股数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.
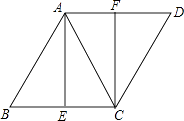
(1)求证:△ABE≌△CDF;
(2)若∠B=60°,AB=4,求线段AE的长.
相关试题

