【题目】
如图,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 。
。
(1)求这两个函数的表达式;
(2)如图1,若![]() ,且其两边分别与两坐标轴的正半轴交于点
,且其两边分别与两坐标轴的正半轴交于点![]() 、点
、点![]() 。求四边形
。求四边形![]() 的面积;
的面积;
(3)如图2,点![]() 是反比例函数
是反比例函数![]() 图象上的一点,过点
图象上的一点,过点![]() 作x轴、
作x轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() ,过
,过![]() 作x轴的垂线,垂足为
作x轴的垂线,垂足为![]() 。设
。设![]() 点的横坐标为
点的横坐标为![]() ,当
,当![]() 时,是否存在点
时,是否存在点![]() ,使得四边形
,使得四边形![]() 为正方形?若存在,求出
为正方形?若存在,求出![]() 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。

参考答案:
【答案】(1)这两个函数的表达式分别为:y=x,![]() ;(2)四边形
;(2)四边形![]() 的面积为6;(3)P点坐标为(
的面积为6;(3)P点坐标为(![]() ,
,![]() )
)
【解析】试题分析:(1)将点M(![]() ,
,![]() )分别带入
)分别带入![]() 与
与![]() 求得a、k的值,即可得这两个函数的表达式;(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D,易证△AMC≌△BMD,S四边形OCMD=S四边形OAMB即可求解;(3)设P点坐标为(
求得a、k的值,即可得这两个函数的表达式;(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D,易证△AMC≌△BMD,S四边形OCMD=S四边形OAMB即可求解;(3)设P点坐标为(![]() ),则PE=HG=GE=
),则PE=HG=GE=![]() ,OE=2x,再由∠MOE=45°,可得OG=GH=
,OE=2x,再由∠MOE=45°,可得OG=GH=![]() , 即可得OE= OG+GH=
, 即可得OE= OG+GH=![]() ,根据正方形的性质可得2x=
,根据正方形的性质可得2x=![]() ,解得x的值,即可求得点P的坐标.
,解得x的值,即可求得点P的坐标.
试题解析:
(1)将点M(![]() ,
,![]() )分别带入
)分别带入![]() 与
与![]() 得:
得:
![]() =a
=a![]() ,
,![]()
解得:a=1,k=6
∴这两个函数的表达式分别为:y=x,![]()
(2)过点M分别做x轴、y轴的垂线,垂足分别为C、D.
则∠MCA=∠MDB=90°,∠AMC=∠BMD=90°-∠AMD,MC=MD=![]() ,
,
∴△AMC≌△BMD,
∴S四边形OCMD=S四边形OMB=6;
(3)设P点坐标为(![]() ),则PE=HG=GE=
),则PE=HG=GE=![]() ,OE=2x,
,OE=2x,
∵∠MOE=45°,∴OG=GH=![]() , ∴OE= OG+GH=
, ∴OE= OG+GH=![]()
∴2x=![]()
![]()
∴P点坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2x+a﹣2=0的解是x=﹣1,则a的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】
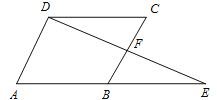
(1)已知:如图,
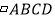 中,延长
中,延长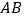 到点
到点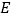 ,使
,使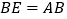 ,连接
,连接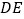 交
交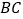 于点
于点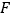 。
。求证:
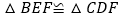 。
。
(2)如图,菱形
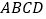 中,对角线
中,对角线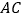 、
、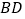 相交于点
相交于点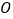 ,已知
,已知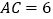 ,
,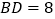 。求菱形
。求菱形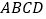 的周长。
的周长。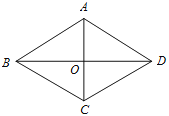
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.
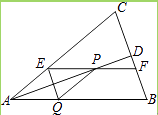
(1)求证:四边形AEPQ为菱形;
(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=
 ,则AB与DE的数量关系是( )
,则AB与DE的数量关系是( )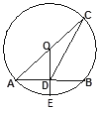
A. AB=2DE B. AB=3DE C. AB=4DE D. 2AB=3DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,我国大约有1.3亿高血压病患者,占15岁以上总人口数的10%﹣15%,预防高血压不容忽视。“千帕kpa”和“毫米汞柱mmHg”都是表示血压的单位,前者是法定的国际计量单位,而后者则是过去一直广泛使用的惯用单位。请你根据下表所提供的信息,判断下列各组换算不正确的是( )
千帕kpa
10
12
16
…
毫米汞柱mmHg
75
90
120
…
A. 18kpa=135mmHg B. 21kpa=150mmHg C. 8kpa=60mmHg D. 32kpa=240mmHg
相关试题

