【题目】如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE. 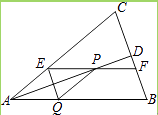
(1)求证:四边形AEPQ为菱形;
(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?
参考答案:
【答案】
(1)证明:∵EF∥AB,PQ∥AC,
∴四边形AEPQ为平行四边形,
∴∠BAD=∠EPA,
∵AB=AC,AD平分∠CAB,
∴∠CAD=∠BAD,
∴∠CAD=∠EPA,
∴EA=EP,
∴四边形AEPQ为菱形.
(2)解:P为EF中点时,S菱形AEPQ= ![]() S四边形EFBQ
S四边形EFBQ
∵四边形AEPQ为菱形,
∴AD⊥EQ,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴EQ∥BC,
又∵EF∥AB,
∴四边形EFBQ为平行四边形.
作EN⊥AB于N,如图所示:
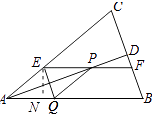
则S菱形AEPQ=EPEN= ![]() EFEN=
EFEN= ![]() S四边形EFBQ.
S四边形EFBQ.
【解析】(1)先证出四边形AEPQ为平行四边形,关键是找一组邻边相等,由AD平分∠BAC和PE∥AQ可证∠EAP=∠EPA,得出AE=EP,即可得出结论;(2)S菱形AEPQ=EPh,S平行四边形EFBQ=EFh,若菱形AEPQ的面积为四边形EFBQ面积的一半,则EP= ![]() EF,因此P为EF中点时,S菱形AEPQ=
EF,因此P为EF中点时,S菱形AEPQ= ![]() S四边形EFBQ .
S四边形EFBQ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2x+a﹣2=0的解是x=﹣1,则a的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】
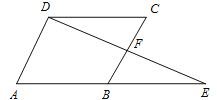
(1)已知:如图,
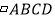 中,延长
中,延长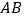 到点
到点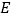 ,使
,使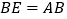 ,连接
,连接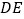 交
交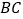 于点
于点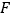 。
。求证:
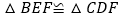 。
。
(2)如图,菱形
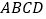 中,对角线
中,对角线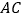 、
、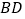 相交于点
相交于点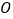 ,已知
,已知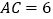 ,
,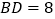 。求菱形
。求菱形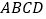 的周长。
的周长。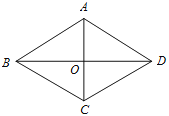
-
科目: 来源: 题型:
查看答案和解析>>【题目】
如图,正比例函数
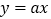 与反比例函数
与反比例函数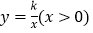 的图象交于点
的图象交于点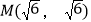 。
。(1)求这两个函数的表达式;
(2)如图1,若
 ,且其两边分别与两坐标轴的正半轴交于点
,且其两边分别与两坐标轴的正半轴交于点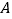 、点
、点 。求四边形
。求四边形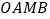 的面积;
的面积;(3)如图2,点
 是反比例函数
是反比例函数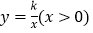 图象上的一点,过点
图象上的一点,过点 作x轴、
作x轴、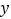 轴的垂线,垂足分别为
轴的垂线,垂足分别为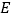 、
、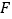 ,
,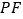 交直线
交直线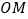 于点
于点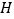 ,过
,过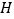 作x轴的垂线,垂足为
作x轴的垂线,垂足为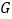 。设
。设 点的横坐标为
点的横坐标为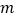 ,当
,当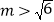 时,是否存在点
时,是否存在点 ,使得四边形
,使得四边形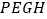 为正方形?若存在,求出
为正方形?若存在,求出 点坐标;若不存在,请说明理由。
点坐标;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是⊙O的直径,AB是⊙O的弦,点E是弧AB的中点,连结OE,交AB于点D,再连结CD,若tan∠CDB=
 ,则AB与DE的数量关系是( )
,则AB与DE的数量关系是( )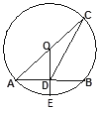
A. AB=2DE B. AB=3DE C. AB=4DE D. 2AB=3DE
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,我国大约有1.3亿高血压病患者,占15岁以上总人口数的10%﹣15%,预防高血压不容忽视。“千帕kpa”和“毫米汞柱mmHg”都是表示血压的单位,前者是法定的国际计量单位,而后者则是过去一直广泛使用的惯用单位。请你根据下表所提供的信息,判断下列各组换算不正确的是( )
千帕kpa
10
12
16
…
毫米汞柱mmHg
75
90
120
…
A. 18kpa=135mmHg B. 21kpa=150mmHg C. 8kpa=60mmHg D. 32kpa=240mmHg
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的4×4方格中,每个小方格的边长都为1
(1)在图(1)中画出长度为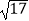 的线段,要求线段的端点在格点上;
的线段,要求线段的端点在格点上;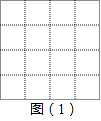
(2)在图(2)中画出一个三条边长分别为3,2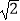 ,
, 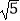 的三角形,使它的端点都在格点上.
的三角形,使它的端点都在格点上.
相关试题

