【题目】某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
参考答案:
【答案】
(1)解:设需要搭配x个A种造型,则需要搭配B种造型(60﹣x)个,
则有 ![]() ,
,
解得37≤x≤40,
所以x=37或38或39或40.
第一种方案:A种造型37个,B种造型23个;
第二种方案:A种造型38个,B种造型22个;
第三种方案:A种造型39个,B种造型21个.
第四种方案:A种造型40个,B种造型20个
(2)解:分别计算四种方案的成本为:
①37×1000+23×1500=71500元,
②38×1000+22×1500=71000元,
③39×1000+21×1500=70500元,
④40×1000+20×1500=70000元.
通过比较可知第④种方案成本最低.
答:选择第四种方案成本最低,最低为70000元
【解析】(1)设需要搭配x个A种造型,则需要搭配B种造型(60﹣x)个,根据“4200盆甲种花卉”“3090盆乙种花卉”列不等式求解,取整数值即可.(2)计算出每种方案的花费,然后即可判断出答案.
【考点精析】根据题目的已知条件,利用一元一次不等式组的应用的相关知识可以得到问题的答案,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.
-
科目: 来源: 题型:
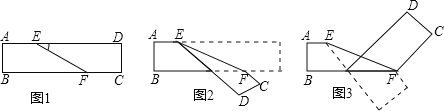
查看答案和解析>>【题目】如图1是长方形纸袋,将纸袋沿EF折叠成图2,再沿BF折叠成图3,若∠DEF=α,用α表示图3中∠CFE的大小为 _________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
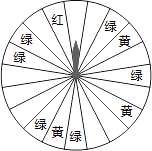
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程4﹣x=2(x+8)的解是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程x+3y=10的非负整数解共有_____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张长方形纸片分别沿着EP,FP对折,使B落在B′,C落在C′.
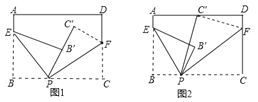
(1)若点P,B′,C′在同一直线上(图1),求两条折痕的夹角∠EPF的度数;
(2)若点P,B′,C′不在同一直线上(图2),且∠B′PC′=10°,求∠EPF的度数.
相关试题

