【题目】计算:(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]() (用乘法公式)
(用乘法公式)
参考答案:
【答案】(1)-5;(2)a8;(3)2a-3b+1;(4)1.
【解析】试题分析:(1)先分别进行绝对值化简,0次幂、负指数幂运算,再按顺序进行计算即可;
(2)先进行积的乘方运算,再进行单项式乘法运算,最后进行合并同类项即可;
(3)利用多项式除以单项式的法则进行计算即可;
(4)2017×2019变为(2018-1)×(2018+1),利用平方差公式进行计算即可得.
试题解析:(1)原式=2+1-8=-5;
(2)原式=a5·(-8a3)+a6·9a2=-8a8+9a8=a8;
(3)原式=2a-3b+1;
(4)原式=20182-(2018-1)×(2018+1)=20182-20182+1=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育老师从七年级学生中抽取40名参加全校的健身操比赛.这些学生身高(单位:cm)的最大值为175,最小值为155.若取组距为3,则可以分成____组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式中,结果等于a5的是( )
A. a2+a3 B. a2a3 C. a5÷a D. (a2)3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果上升10米记作+10米,那么下降5米记作_______米.
-
科目: 来源: 题型:
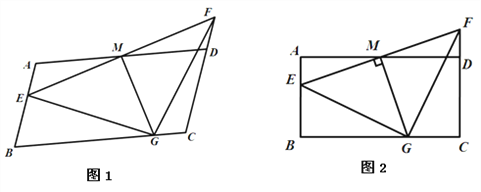
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=2,AD=4,M是AD的中点,点E是线段AB上一动点(可以运动到点A和点B),连接EM并延长交线段CD的延长线于点F.
(1) 如图1,①求证:AE=DF; ②若EM=3,∠FEA=45°,过点M作MG⊥EF交线段BC于点G,请直接写出△GEF的的形状,并求出点F到AB边的距离;
(2)改变平行四边形ABCD中∠B的度数,当∠B=90°时,可得到矩形ABCD(如图2),请判断△GEF的形状,并说明理由;
(3)在(2)的条件下,取MG中点P,连接EP,点P随着点E的运动而运动,当点E在线段AB上运动的过程中,请直接写出△EPG的面积S的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点O在AC上,OA=2,以OA为半径的⊙O交AB于点D,AC于G,BD的垂直平分线交BC于点E,交BD于点F,连接DE.

(1)求证:直线DE是⊙O的切线;
(2)求线段DE的长;
(3)求线段AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.

相关试题

