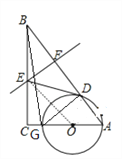
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点O在AC上,OA=2,以OA为半径的⊙O交AB于点D,AC于G,BD的垂直平分线交BC于点E,交BD于点F,连接DE.

(1)求证:直线DE是⊙O的切线;
(2)求线段DE的长;
(3)求线段AD的长.
参考答案:
【答案】(1)证明见解析(2)DE=4.75(3)2.4
【解析】试题分析:(1)连接OD,欲证DE是切线,只要证明OD⊥DE即可;
(2)连接OE,设DE=BE=x,CE=8﹣x,利用勾股定理求解即可;
(3)连结BG,DG,根据三角形的面积的不同求法,然后根据勾股定理求解.
试题解析:(1)连接OD,
∵EF垂直平分BD,∴EB=ED,
∴∠B=∠EDB,
∵OA=OD,∴∠ODA=∠A,
∵∠C=90°,∴∠A+∠B=90°,
∴∠EDB+∠ODA=90°,∴∠ODE=90°,
∴OD⊥DE于D,∴DE是⊙O的切线.
(2)连接OE,
设DE=BE=x,CE=8﹣x,
∵OE2=DE2+OD2=EC2+OC2,
∴42+(8﹣x)2=22+x2,
解得x=4.75,
 ∴DE=4.75.
∴DE=4.75.
(3)连结BG,DG.
∵AG是直径,∴GD⊥AB
由S△ABG=![]() AG·BC=
AG·BC=![]() AB·GD可得:4×8=10×GD,
AB·GD可得:4×8=10×GD,
∴GD=3.2
∴AD=![]() =2.4
=2.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果上升10米记作+10米,那么下降5米记作_______米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
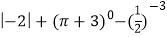 (2)
(2)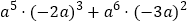
(3)
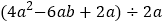 (4)
(4)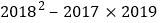 (用乘法公式)
(用乘法公式) -
科目: 来源: 题型:
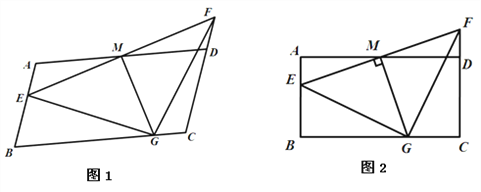
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=2,AD=4,M是AD的中点,点E是线段AB上一动点(可以运动到点A和点B),连接EM并延长交线段CD的延长线于点F.
(1) 如图1,①求证:AE=DF; ②若EM=3,∠FEA=45°,过点M作MG⊥EF交线段BC于点G,请直接写出△GEF的的形状,并求出点F到AB边的距离;
(2)改变平行四边形ABCD中∠B的度数,当∠B=90°时,可得到矩形ABCD(如图2),请判断△GEF的形状,并说明理由;
(3)在(2)的条件下,取MG中点P,连接EP,点P随着点E的运动而运动,当点E在线段AB上运动的过程中,请直接写出△EPG的面积S的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把两个三角形按如图1放置,其中∠ACB=∠DEC=90°,∠CAB=45°,∠CDE=30°,且AB=6,DC=7,把△DCE绕点C顺时针旋转15°得△D1CE1,如图2,这时AB与CD1相交于点O、与D1E1相交于点F;

(1)求∠ACD1的度数;
(2)求线段AD1的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用普查的是( )
A.了解淮坊市民对建设高铁的意见
B.了解同一批电脑的使用寿命
C.检查一枚用于发射卫星的运载火箭的各个零部件
D.了解淮坊市汽车驾驶员对礼让行人的意识
相关试题

