Question

【题目】如图，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+b）2+|a-b+4|=0，过点C作CB⊥x轴于B.

（1）如图1，求△ABC的面积.

（2）如图2，若过B作BD∥AC交y轴于D，在△ABC内有一点E，连接AE.DE，若∠CAE+∠BDE=∠EAO+∠EDO，求∠AED的度数.

（3）如图3，在（2）的条件下，DE与x轴交于点M，AC与y轴交于点F，作△AME的角平分线MP，在PE上有一点Q，连接QM，∠EAM+2∠PMQ=45°，当AE=2AM，FO=2QM时，求点E的纵坐标.

Answer 1

【答案】（1）4；（2）45°；（3）1

【解析】

（1）由题意可求a=-2，b=2，即可得点A，点C坐标，即可求△ABC的面积；

（2）根据题意可求∠CAE+∠BDE=∠EAO+∠EDO=45°，根据三角形内角和可求∠AED的度数；

（3）如图3，先根据三角形的中位线定理可得：QM=，过E作EG⊥x轴于G，设∠PMQ=x，则∠EAM=45-2x，证明MQ⊥AE，利用面积法可得：S△AEM=AEMQ＝AMEG，可得EG=1，即点E的纵坐标是1．

（1）∵（a+b）2≥0，|a-b+4|≥0，（a+b）2+|a-b+4|=0，

∴a=-b，a-b+4=0，

∴a=-2，b=2，

∵CB⊥AB

∴A（-2，0），B（2，0），C（2，2），

∴△ABC的面积=×4×2=4；

（2）如图2，连接AD，

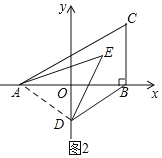
∵BD∥AC，

∴∠CAD+∠BDA=180°，

∵∠OAD+∠ODA=90°，

∴∠CAB+∠BDO=90°，

∵∠CAE+∠BDE=∠EAO+∠EDO，

∴∠CAE+∠BDE=∠EAO+∠EDO=45°，

△ADE中，∠AED=180°-（∠EAO+∠EDO）-（∠OAD+∠ODA）=180°-45°-90°=45°；

（3）如图3，

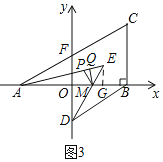
∵OF∥BC，OA=OB=2，

∴AF=FC，

∴OF=BC=1，

∵OF=2QM，

∴QM=，

过E作EG⊥x轴于G，

设∠PMQ=x，则∠EAM=45-2x，

由（2）知：∠EAM+∠EDO=45°，

∴∠EDO=45°-（45°-2x）=2x，

∴∠EMG=∠OMD=90°-2x，

∵PM平分∠AME，

∴∠AMP=∠PME==45°+x，

∴∠QPM=∠EAM+∠AMP=45°-2x+45°+x=90°-x，

∴∠QPM+∠PMQ=90°，

∴MQ⊥AE，

S△AEM=AEMQ＝AMEG，

∵AE=2AM，

∴2AM=AMEG，

∴EG=1,即点E的纵坐标是1．