【题目】如图,![]() 中,
中,![]() 和
和![]() 分别平分
分别平分![]() 和
和![]() 的外角
的外角![]() ,一动点
,一动点![]() 在
在![]() 上运动,过点
上运动,过点![]() 作
作![]() 的平行线与
的平行线与![]() 和
和![]() 的角平分线分别交于点
的角平分线分别交于点![]() 和点
和点![]() .
.

![]() 求证:当点
求证:当点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 为矩形,说明理由;
为矩形,说明理由;
![]() 在第
在第![]() 题的基础上,当
题的基础上,当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 为正方形,说明理由.
为正方形,说明理由.
参考答案:
【答案】(1)当点![]() 运动到
运动到![]() 的中点位置时,四边形
的中点位置时,四边形![]() 为矩形;理由见解析;(2)当
为矩形;理由见解析;(2)当![]() 时,四边形
时,四边形![]() 为正方形,理由见解析
为正方形,理由见解析
【解析】
(1)利用角平分线的性质以及平行线的性质得出OE=OF,即可得出结论;
(2)证出EF⊥AC,即可得出结论.
![]() 证明:当点
证明:当点![]() 运动到
运动到![]() 的中点位置时,四边形
的中点位置时,四边形![]() 为矩形;理由如下:
为矩形;理由如下:
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可证,![]() ,
,
∴![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形;
为矩形;
![]() 解:当
解:当![]() 时,四边形
时,四边形![]() 为正方形;
为正方形;
理由如下:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 为矩形,
为矩形,
∴四边形![]() 为正方形.
为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
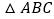 中,点
中,点 、
、 、
、 分别在
分别在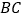 、
、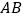 、
、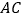 上,且
上,且 ,
, .
.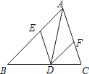
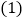 如果
如果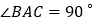 ,那么四边形
,那么四边形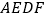 是________形;
是________形;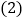 如果
如果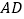 是
是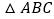 的角平分线,那么四边形
的角平分线,那么四边形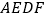 是________形.
是________形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,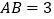 ,
,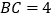 ,点
,点 是对角线
是对角线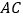 上的动点(不与
上的动点(不与 、
、 重合),设
重合),设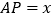 ,
, .
.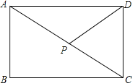
 求
求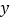 与
与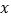 的函数解析式,并指出
的函数解析式,并指出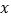 的取值范围;
的取值范围; 连接
连接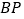 ,当
,当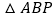 是等腰三角形时,求
是等腰三角形时,求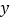 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 、
、 分别是
分别是 、
、 的中点,
的中点, 、
、 分别是
分别是 、
、 的中点.
的中点.
 求证:四边形
求证:四边形 是菱形;
是菱形; 若
若 ,
, ,求四边形
,求四边形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并完成任务。
筝形的定义:两组邻边分别相等的四边形叫做筝形,几何图形的定义通常可作为图形的性质也可以作为图形的判定方法.也就是说,如图,若四边形ABCD是一个筝形,则AB=AD,BC=CD;若AB=AD,BC=CD,则四边形ABCD是筝形.
如图,四边形ABCD是一个筝形,其中AB=AD,BC=CD.对角线AC,BD相交于点O,过点0作0M⊥AB,ON⊥AD,垂足分别为M,N.求证:四边形AMON是筝形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,将两个全等的三角板如图摆放,其中△ABC和ΔADE的直角顶点重合在点A处,∠ADE=∠ABC=60°,且点D在AC上,点B在AE上,∠C=∠E=30°,AB=AD,AC=AE,BC=DE,BC和DE相交于点F.求证:CF=EF.

(2)如图2,将这两个三角板如图摆放,直角顶点A仍然重合,BC与DE相交于点F,AC与DE交于点M,AE和BC交于点N.猜想CF和EF还相等吗?说明理由.
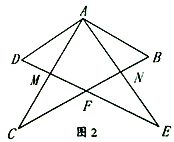
(3)如图3,在(2)的基础上,若∠DAM=30°.求证:线段DF和AC互相垂直平分.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,点
中,点 是
是 上任意一点,以
上任意一点,以 为边作正方形
为边作正方形 .
.①连接
 ,求证:
,求证: ;
;②连接
 ,猜想
,猜想 的度数,并证明你的结论;
的度数,并证明你的结论;③设点
 在线段
在线段 上运动,
上运动, ,正方形
,正方形 的面积为
的面积为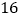 ,正方形
,正方形 的面积为
的面积为 ,试求
,试求 与
与 的函数关系式,并写出
的函数关系式,并写出 的取值范围.
的取值范围.
相关试题

