【题目】为了解学生的艺术特长发展情况,某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了名学生,其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 . 扇形统计图中喜欢“戏曲”部分扇形的圆心角为度.
(2)请你补全条形统计图.
(3)若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率.
参考答案:
【答案】
(1)50;24%;28.8
(2)解:补全统计图如图:

(3)解:画树状图如下:

∵共有12种等可能结果,其中恰好选中“舞蹈、声乐”这两项活动的有2种结果,
故恰好选中“舞蹈、声乐”两项活动的概率是: ![]() =
= ![]() .
.
【解析】解:(1)一共抽查学生数为:8÷16%=50,
“舞蹈”活动项目的人数占抽查总人数的百分比为: ![]() ×100%=24%;
×100%=24%;
∵喜欢戏曲的人数:50﹣12﹣16﹣8﹣10=50﹣46=4人,
∴扇形统计图中喜欢“戏曲”部分扇形的圆心角为: ![]() ×360°=28.8°,
×360°=28.8°,
故答案为:50,24%,28.8.
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.(1)用喜欢声乐的人数除以所占的百分比,进行计算即可得解;用喜欢舞蹈的人数除以被抽查的总人数即可;求出喜欢戏曲的人数,用戏曲人数所占比例乘以360°可得;(2)由(1)中求得的戏曲人数,补全统计图即可;(3)画出树状图,然后根据概率公式列式进行计算即可得解
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=﹣
 x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 .
x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|
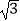 -
-  |+(
|+(  -1)0+2sin45°﹣2cos30°+(
-1)0+2sin45°﹣2cos30°+(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.

(1)求证:四边形CMAN是平行四边形.
(2)已知DE=4,FN=3,求BN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(k﹣1)x2+2kx+2=0.
(1)求证:无论k为何值,方程总有实数根.
(2)设x1 , x2是方程(k﹣1)x2+2kx+2=0的两个根,记S=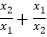 +x1+x2 , S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
+x1+x2 , S的值能为2吗?若能,求出此时k的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60(
 +
+ 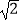 )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(
)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120(  -
- 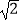 )海里.
)海里.
(参考数据: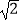 =1.41,
=1.41,  =1.73,
=1.73,  =2.45)
=2.45)
(1)分别求出A与C及B与C的距离AC、BC(结果保留根号)
(2)已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
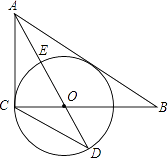
(1)求证:AB是⊙O的切线.
(2)已知AO角⊙O于点E,延长AO交⊙O于点D,tanD= ,求
,求 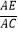 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
相关试题

