【题目】如图,直线l:y=﹣ ![]() x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 .
x,点A1坐标为(﹣3,0).过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3 , …,按此做法进行下去,点A2016的坐标为 . 
参考答案:
【答案】![]()
【解析】解:∵点A1坐标为(﹣3,0),
∴OA1=3,
∵在y=﹣ ![]() x中,当x=﹣3时,y=4,即B1点的坐标为(﹣3,4),
x中,当x=﹣3时,y=4,即B1点的坐标为(﹣3,4),
∴由勾股定理可得OB1= ![]() =5,即OA2=5=3×
=5,即OA2=5=3× ![]() ,
,
同理可得,
OB2= ![]() ,即OA3=
,即OA3= ![]() =3×(
=3×( ![]() )2 ,
)2 ,
OB3= ![]() ,即OA4=
,即OA4= ![]() =3×(
=3×( ![]() )3 ,
)3 ,
以此类推,
OAn=3×( ![]() )n﹣1=
)n﹣1= ![]() ,即点An坐标为(﹣
,即点An坐标为(﹣ ![]() ,0),
,0),
当n=2016时,点A2016坐标为(﹣ ![]() ,0).
,0).
所以答案是:(﹣ ![]() ,0)
,0)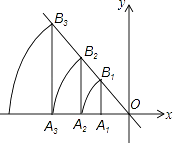
【考点精析】认真审题,首先需要了解一次函数的性质(一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )

A.5
B.7
C.8
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=
 的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+
的图象相交于A(﹣2,m)、B(1,n)两点,连接OA、OB,给出下列结论:①k1k2<0;②m+  n=0;③S△AOP=S△BOQ;④不等式k1x+b
n=0;③S△AOP=S△BOQ;④不等式k1x+b  的解集是x<﹣2或0<x<1,其中正确的结论的序号是 .
的解集是x<﹣2或0<x<1,其中正确的结论的序号是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|
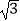 -
-  |+(
|+(  -1)0+2sin45°﹣2cos30°+(
-1)0+2sin45°﹣2cos30°+(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.

(1)求证:四边形CMAN是平行四边形.
(2)已知DE=4,FN=3,求BN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生的艺术特长发展情况,某校音乐决定围绕在“舞蹈、乐器、声乐、戏曲、其他活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.请你根据统计图解答下列问题:

(1)在这次调查中,一共抽查了名学生,其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 . 扇形统计图中喜欢“戏曲”部分扇形的圆心角为度.
(2)请你补全条形统计图.
(3)若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率.
相关试题

