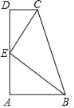
【题目】如图,AB∥CD,∠A=90°,E是AD边中点,CE平分∠BCD.
(1)求证:BE平分∠ABC;
(2)若AB=2,CD=1,求BC长;
(3)若△BCE的面积为6,求四边形ABCD的面积.
参考答案:
【答案】(1)证明见解析;(2)BC=3;(3)12.
【解析】
(1)作EM⊥BC垂足为M,根据角平分线的判定与性质即可得证;
(2)通过HL证明Rt△CDE≌Rt△CME与Rt△BAE≌Rt△BNE,可得CM=CD,BM=AB,然后相加即可得解;
(3)根据(2)可知Rt△CDE≌Rt△CME与Rt△BAE≌Rt△BNE,则四边形ABCD的面积为△BCE面积的2倍.
(1)证明:作EM⊥BC垂足为M,
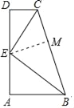
∵EC平分∠DCB,ED⊥CD,EM⊥BC,
∴ED=EM,
∵AE=ED,
∴EA=EM,
∵EA⊥AB,EM⊥BC,
∴EB平分∠ABC;
(2)证明:由(1)可知:AE=EM=ED,
在Rt△DEC和Rt△CEM中,
![]() ,
,
∴△ECD≌△ECM(HL))
∴DC=CM,
同理可证:AB=BM,
∴BC=CM+MM=CD+AB=3;
(3)解:由(2)可知:△ECD≌△ECM(HL),
∴S△ECD=S△ECM,同法可证:S△EBM=S△EBA,
∴S四边形ABCD=2S△BEC,
∵△BCE的面积为6,
∴四边形ABCD的面积为12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】求一个正数的算术平方根,有些数可以直接求得,如
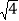 ;有些数则不能直接求得,如
;有些数则不能直接求得,如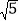 ,除通过计算器可以求得外,还可以通过一组数的内在联系,运用规律求得,观察下表:
,除通过计算器可以求得外,还可以通过一组数的内在联系,运用规律求得,观察下表:n
0.09
9
900
90000
…
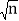
0.3
3
30
300
…
(1)根据表中的规律,可以求得
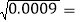 ____,
____,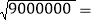 ____;
____;(2)根据表中的规律,还可以由
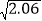 ≈1.435,求得
≈1.435,求得 ≈____,
≈____,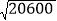 ≈____,
≈____,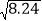 ≈____.
≈____. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究一次函数y=kx+k+2(k是不为0常数)图象的共性特点,探究过程:小明尝试把x=﹣1代入时,发现可以消去k,竟然求出了y=2.老师问:结合一次函数图象,这说明了什么?小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过定点(﹣1,2),老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.已知一次函数y=(k+3)x+(k﹣1)的图象是“点选直线”
(1)一次函数y=(k+3)x+(k﹣1)的图象经过的顶点P的坐标是 .
(2)已知一次函数y=(k+3)x+(k﹣1)的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3,求k值;
②若△AOB的面积为1,求k值.
-
科目: 来源: 题型:
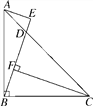
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,D是AC上一点,AE⊥BD,交BD的延长线于E,CF⊥BD于F.
(1)求证:CF=BE;
(2)若BD=2AE,求证:∠EAD=∠ABE.
-
科目: 来源: 题型:
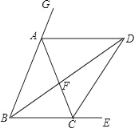
查看答案和解析>>【题目】如图,已知在△ABC中,AD、BD分别平分∠CAG、∠EBA,AD∥BC,BD交AC于F,连接CD,
(1)求证:AB=AC.
(2)当∠EBA的大小满足什么条件时,以A,B,F为顶点三角形为等腰三角形?
(3)猜想∠BDC与∠DAC之间的数量关系式,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,添加以下条件,不能判定
,添加以下条件,不能判定 的是( )
的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
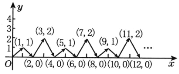
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律,经过第2015次运动后,动点P的坐标是____.
相关试题

