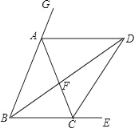
【题目】如图,已知在△ABC中,AD、BD分别平分∠CAG、∠EBA,AD∥BC,BD交AC于F,连接CD,
(1)求证:AB=AC.
(2)当∠EBA的大小满足什么条件时,以A,B,F为顶点三角形为等腰三角形?
(3)猜想∠BDC与∠DAC之间的数量关系式,并说明理由.
参考答案:
【答案】(1)详见解析;(2)∠EBA=72°或![]() 时,△ABF为等腰三角形;(3)∠BDC+∠DAC=90°.
时,△ABF为等腰三角形;(3)∠BDC+∠DAC=90°.
【解析】
(1)根据平行线的性质可得∠GAD=∠ABC,∠ACB=∠CAD,即∠ABC=∠ACB,则AB=AC;
(2)分①AB与AF不可能相等;②当AF=BF时,③AB=BF时,三种情况讨论,根据三角形的内角和定理进行求解即可;
(3)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H,根据三角形的外角等于其不相邻的两个内角和,可得∠BDC=∠DCH﹣∠DBH=![]() ∠ACH﹣
∠ACH﹣![]() ∠ABH=
∠ABH=![]() (∠ACH﹣∠ABH)=
(∠ACH﹣∠ABH)=![]() ∠BAC,因为∠DAC=
∠BAC,因为∠DAC=![]() ×(180°﹣∠A)=90°﹣
×(180°﹣∠A)=90°﹣![]() ∠BAC,所以∠BDC+∠DAC=90°.
∠BAC,所以∠BDC+∠DAC=90°.
(1)证明:∵AD平分∠CAG,
∴∠GAD=∠CAD,
∵AD∥BC,
∴∠GAD=∠ABC,∠ACB=∠CAD,
∴∠ABC=∠ACB,
∴AB=AC;
(2))①AB与AF不可能相等;
②当AF=BF时,∠BAF=∠ABF=![]() ∠ABC,
∠ABC,
∵∠BAC+∠ABC+∠ACB=180°,∠ABC=∠ACB,
∴![]() ∠ABC=180°,
∠ABC=180°,
∴∠ABC=72°;
③AB=BF时,设∠ABF=∠FBC=x,
则∠ABC=∠ACB=2x,
∴∠BAF=∠BFA=3x,
∴2x+2x+3x=180°,
∴x=![]() ,
,
∴∠EBA=2x=![]() ,
,
综上所述,当∠EBA=72°或![]() 时,△ABF为等腰三角形;
时,△ABF为等腰三角形;
(3)∠BDC+∠DAC=90°,
理由如下:作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H,
∵AD、BD分别平分∠GAC、∠EBA,DM⊥BG,DN⊥AC,DH⊥BE,
∴DM=DN,DM=DH,
∴DH=DN,
又∵DN⊥AC,DH⊥BE,
∴CD平分∠ADH,即∠DCH=![]() ∠ACH,
∠ACH,
∴∠BDC=∠DCH﹣∠DBH=![]() ∠ACH﹣
∠ACH﹣![]() ∠ABH=
∠ABH=![]() (∠ACH﹣∠ABH)=
(∠ACH﹣∠ABH)=![]() ∠BAC,
∠BAC,
∵∠DAC=![]() ×(180°﹣∠A)=90°﹣
×(180°﹣∠A)=90°﹣![]() ∠BAC,
∠BAC,
∴∠BDC+∠DAC=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究一次函数y=kx+k+2(k是不为0常数)图象的共性特点,探究过程:小明尝试把x=﹣1代入时,发现可以消去k,竟然求出了y=2.老师问:结合一次函数图象,这说明了什么?小组讨论得出:无论k取何值,一次函数y=kx+k+2的图象一定经过定点(﹣1,2),老师:如果一次函数的图象是经过某一个定点的直线,那么我们把像这样的一次函数的图象定义为“点旋转直线”.已知一次函数y=(k+3)x+(k﹣1)的图象是“点选直线”
(1)一次函数y=(k+3)x+(k﹣1)的图象经过的顶点P的坐标是 .
(2)已知一次函数y=(k+3)x+(k﹣1)的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3,求k值;
②若△AOB的面积为1,求k值.
-
科目: 来源: 题型:
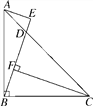
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,D是AC上一点,AE⊥BD,交BD的延长线于E,CF⊥BD于F.
(1)求证:CF=BE;
(2)若BD=2AE,求证:∠EAD=∠ABE.
-
科目: 来源: 题型:
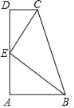
查看答案和解析>>【题目】如图,AB∥CD,∠A=90°,E是AD边中点,CE平分∠BCD.
(1)求证:BE平分∠ABC;
(2)若AB=2,CD=1,求BC长;
(3)若△BCE的面积为6,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,添加以下条件,不能判定
,添加以下条件,不能判定 的是( )
的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
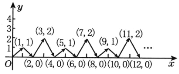
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)…按这样的运动规律,经过第2015次运动后,动点P的坐标是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )
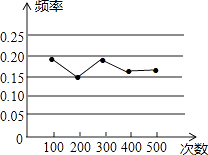
A.同时抛掷两枚硬币,落地后两枚硬币正面都朝上
B.一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃
C.抛一个质地均匀的正方体骰子,朝上的面点数是3
D.一个不透明的袋子中有4个白球、1个黑球,它们除了颜色外都相同,从中抽到黑球
相关试题

