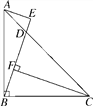
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,D是AC上一点,AE⊥BD,交BD的延长线于E,CF⊥BD于F.
(1)求证:CF=BE;
(2)若BD=2AE,求证:∠EAD=∠ABE.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】(1)根据已知条件证明△ABE≌△BCF即可求证CF=BE.
(2)由(1)可知:∠ABE=∠BCF,且AE∥CF所以∠EAD=∠ACF,只需证明∠ABE=∠BCF=∠ACF即可证明出∠EAD=∠ABE.
证明:(1)∵∠ABC=90°,CF⊥BD,AE⊥BD,
∴∠ABE+∠EBC=90°=∠EBC+∠BCF,
∴∠ABE=∠BCF.
又∵∠AEB=∠BFC=90°,AB=CB,
∴△ABE≌△BCF,
∴CF=BE.
(2)由(1)知△ABE≌△BCF,
∴BF=AE,∠ABE=∠BCF.又∵BD=BF+FD=2AE,
∴BF=DF.
又∵CF⊥BD于F,∴CB=CD,
∴CF平分∠ACB.
又∵∠AEB=∠CFD=90°,
∴AE∥CF,∴∠EAD=∠ACF.
∵∠ABE=∠BCF=∠ACF,
∴∠EAD=∠ABE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算与解方程组
(1)( )﹣2+|2
)﹣2+|2 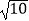 ﹣6|﹣
﹣6|﹣ 
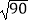 ;
;
(2)解方程组: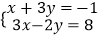 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣3x+m﹣3=0,若此方程的两根的倒数和为1,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格?
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年来全国各省市市政府民生实事之一的公共自行车建设工作已基本完成,网上资料显示呼和浩特市某部门对14年4月份中的7天进行了公共自行车日租车辆的统计,结果如图:
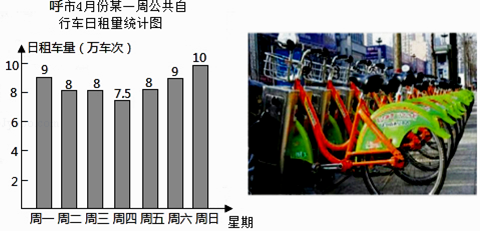
(1)求这7天日租车量的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)该市共租车多少万车次;
(3)资料显示,呼市政府在公共自行车建设项目中共投入9600万元,估计2014年共租车3200万车次,每车次平均收入租车费0.1元,求2014年该市租车费收入占总投入的百分率(精确到0.1%).
相关试题

