【题目】如图,平面直角坐标系中,△ABC≌△DEF, AB=BC=5.若A点的坐标为(﹣3,1),B、C两点在直线y=﹣3上,D、E两点在y轴上,则点F的横坐标为( )
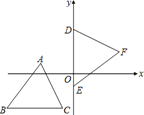
A. 2 B. 3 C. 4 D. 5
参考答案:
【答案】C
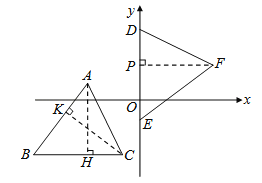
【解析】分析:如图,作AH、CK、FP分别垂直BC、AB、DE于H、K、P.由AB=BC,△ABC≌△DEF,就可以得出△AKC≌△CHA≌△DPF,就可以得出结论.
详解:如图,作AH、CK、FP分别垂直BC、AB、DE于H、K、P,∴∠DPF=∠AKC=∠CHA=90°.
∵AB=BC,∴∠BAC=∠BCA.
在△AKC和△CHA中,
∵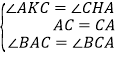 ,∴△AKC≌△CHA(ASA),∴KC=HA.
,∴△AKC≌△CHA(ASA),∴KC=HA.
∵B、C两点在方程式y=﹣3的图形上,且A点的坐标为(﹣3,1),∴AH=4,∴KC=4.
∵△ABC≌△DEF,∴∠BAC=∠EDF,AC=DF.
在△AKC和△DPF中,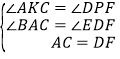 ,∴△AKC≌△DPF(AAS),∴KC=PF=4.
,∴△AKC≌△DPF(AAS),∴KC=PF=4.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
如图,将矩形
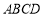 的四边
的四边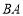 、
、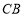 、
、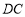 、
、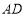 分别延长至
分别延长至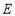 、
、 、
、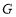 、
、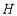 ,使得
,使得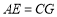 ,
,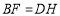 ,连接
,连接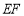 ,
,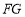 ,
,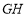 ,
,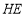 .
.(1) 求证:四边形
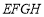 为平行四边形;
为平行四边形;(2) 若矩形
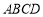 是边长为1的正方形,且
是边长为1的正方形,且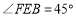 ,
,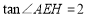 ,求
,求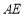 的长.
的长.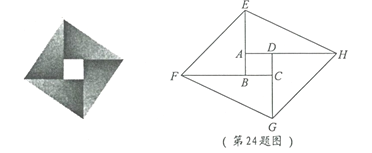
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
(提出问题)三个有理数
 、
、 、
、 满足
满足 ,求
,求 的值.
的值.(解决问题)
解:由题意,得
 、
、 、
、 三个有理数都为正数或其中一个为正数,另两个为负数,
三个有理数都为正数或其中一个为正数,另两个为负数,①
 、
、 、
、 都是正数,即
都是正数,即 、
、 、
、 时,则
时,则 :
:②当
 、
、 、
、 中有一个为正数,另两个为负数时,不妨设
中有一个为正数,另两个为负数时,不妨设 、
、 、
、 ,则,
,则, ,综上所述,
,综上所述, 值为
值为 或
或 .
.(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数
 、
、 、
、 满足
满足 ,求
,求 的值;
的值;(2)若
 、
、 、
、 为三个不为
为三个不为 的有理数,且
的有理数,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A、B、C三点分别对应实数a、1、c,且BC-AB=AC.下列选项中,满足A、B、C三点在数轴上的位置关系是( )
A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
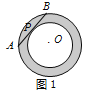
查看答案和解析>>【题目】(1)如图1,同心圆中,大圆O的弦AB与小圆O切于点P,且AB=16,则圆环面积为________;
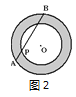
(2)如图2,同心圆中,大圆O的弦AB与小圆O相交,其中一个交点为点P,且AP=2,PB=8,则圆环面积为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如图,点D是折线A﹣C﹣B的“折中点”,请解答以下问题:

(1)当AC>BC时,点D在线段 上; 当AC=BC时,点D与 重合;当AC<BC时,点D在线段 上;
(2)若AC=18cm,BC=10cm,若∠ACB=90°,有一动点P从C点出发,在线段CB上向点B运动,速度为2cm/s, 设运动时间是t(s), 求当t为何值,三角形PCD 的面积为10
 ?
?(3)若E为线段AC中点,EC=8cm,CD=6cm,求CB的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
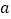 克糖水中有
克糖水中有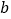 克糖(
克糖(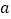 >
>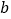 >0),则糖的质量与糖水的质量比为_______;若再添加
>0),则糖的质量与糖水的质量比为_______;若再添加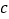 克糖,并全部溶解(
克糖,并全部溶解(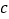 >0),则糖的质量与糖水的质量比为__________;生活常识告诉我们,添加的糖完全溶解后,糖水会更甜,因此我们可以猜想出以上两个质量比之间的大小关系是______________;
>0),则糖的质量与糖水的质量比为__________;生活常识告诉我们,添加的糖完全溶解后,糖水会更甜,因此我们可以猜想出以上两个质量比之间的大小关系是______________;(2)我们的猜想正确吗?请你证明这个猜想。
相关试题

