【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如图,点D是折线A﹣C﹣B的“折中点”,请解答以下问题:

(1)当AC>BC时,点D在线段 上; 当AC=BC时,点D与 重合;当AC<BC时,点D在线段 上;
(2)若AC=18cm,BC=10cm,若∠ACB=90°,有一动点P从C点出发,在线段CB上向点B运动,速度为2cm/s, 设运动时间是t(s), 求当t为何值,三角形PCD 的面积为10![]() ?
?
(3)若E为线段AC中点,EC=8cm,CD=6cm,求CB的长度.
参考答案:
【答案】(1)AC,C,BC; (2) ![]() s;(3)CB的长度是4cm或28cm.
s;(3)CB的长度是4cm或28cm.
【解析】试题分析:(1)根据图形以及阅读材料所给的信息直接填空即可;(2)如图4,先表示PC=2t,由折中点的定义得AD=14,根据三角形的面积公式列式可求t的值;(3)分当点D在线段AC上与BC上两种情况求解即可.
试题解析:
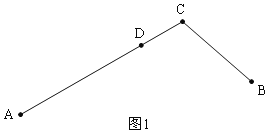
(1)当AC>BC时,如图1,点D在线段AC上;
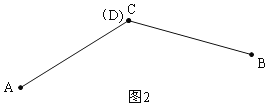
当AC=BC时,如图2,点D与C重合;
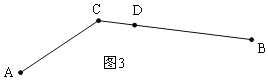
当AC<BC时,如图3,点D在线段BC上;
因此,本题正确答案是:AC,C,BC.
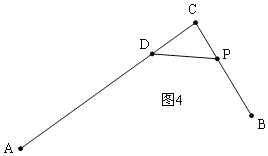
(2)如图4,根据题意得:PC=2t,
∵AC=18,BC=10 cm,
∴AC+BC=18+10=28 cm,
∵D点是折中点,
∴AD=14cm,
∴CD=18-14=4cm,
∵∠ACB=90°,
∴![]() ,
,
即![]() ,
,
解得![]() ,
,
则当t为![]() 秒时,三角形PCD的面积为10cm2;
秒时,三角形PCD的面积为10cm2;
(3)分两种情况:
①点D在线段AC上时,如图5,
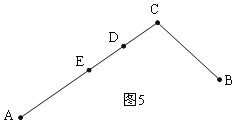
∵E为线段AC中点,EC=8 cm,
∴AC=2CE=16cm,
∵CD=6cm,
∴AD=AC-CD=16-6=10cm,
∵D为折中点,
∴AD=CD+BC,
∴BC=AD-CD=10-6=4cm;
②点D在线段BC上,如图6,
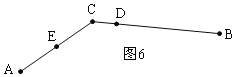
∵E为线段AC中点,EC=8cm,
∴AC=2CE=16cm,
∴AD=AC+CD=16+6=22cm,
∴BD=AC+CD=22cm,
∴BC=BD+CD=22+6=28cm.
综上所述,CB的长度是4 cm 或28 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于反比例函数y=
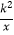 (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A.它的图像分布在第一、三象限
B.点(k,k)在它的图像上
C.它的图像关于原点对称
D.在每个象限内y随x的增大而增大 -
科目: 来源: 题型:
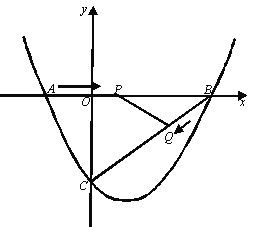
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
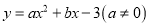 与x轴交于点A(
与x轴交于点A(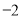 ,0)、B(4,0)两点,与y轴交于点C。
,0)、B(4,0)两点,与y轴交于点C。(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度向C点运动。其中一个点到达终点时,另一个点也停止运动。当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最多面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK∶S△PBO=5∶2,求K点坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名学生军训时连续射靶10次,命中环数分别为 7,8,6,8,5,9,10,7,6,4.则这名学生射击环数的方差是( )
A. 3 B. 2.9 C. 2.8 D. 2.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明妈妈经营一家服装专卖店,为了合理利用资金,小明帮妈妈对上个月各种型号的服装销售数量进行了一次统计分析,决定在这个月的进货中多进某种型号服装,此时小明应重点参考( )
A. 众数 B. 平均数 C. 加权平均数 D. 中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,∠AOB和∠COD都是直角
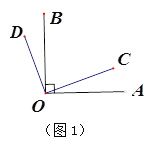
①若∠BOC=60°,则∠BOD= °,∠AOC= °;
②改变∠BOC的大小,则∠BOD与∠AOC相等吗?为什么?
(2)如图2,∠AOB=∠COD=80°,若∠AOD=∠BOC+40°,求∠AOC的度数;
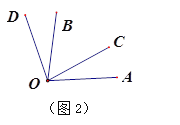
(3)如图3,将三个相同的等边三角形(三个内角都是60°)的一个顶点重合放置,若∠BAE=10°, ∠HAF=30°,则∠1= °.
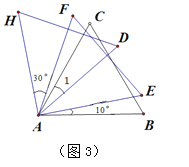
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运20千克,A型机器人搬运1000千克所用时间与B型机器人搬运800千克所用时间相等,两种机器人每小时分别搬运多少化工原料?
相关试题

