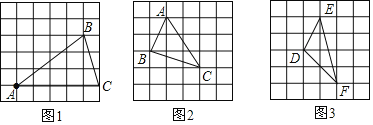
【题目】(1)正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使AB=AC=5,BC=![]()
(2)在△ABC中, AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图2所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图2所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
①△ABC的面积为: .
②若△DEF三边的长分别为![]() 、
、![]() 、
、![]() ,请在图3的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为_____________.
,请在图3的正方形网格中画出相应的△DEF,并利用构图法求出它的面积为_____________.

参考答案:
【答案】(1)作图见解析;(2)①3.5;②作图见解析,3
【解析】试题分析:(1)根据勾股定理画出图形即可;
(2)①利用△ABC所在的正方形的面积减去四周三个小直角三角形的面积,计算即可得解;
②根据网格结构和勾股定理作出△DEF,再利用△DEF所在的矩形的面积减去四周三个小直角三角形的面积,计算即可得解
试题解析: (1)如图1所示,△ABC即为所求;
(2)①![]() =3×3
=3×3![]() ×2×1
×2×1![]() ×3×1
×3×1![]() ×2×3=91
×2×3=91![]() 3=3.5,
3=3.5,
②如图3,△DEF即为所求,![]() =2×4
=2×4![]() ×1×2
×1×2![]() ×2×2
×2×2![]() ×1×4=8122=85=3.
×1×4=8122=85=3.
-
科目: 来源: 题型:
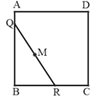
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,将长为4的线段QR的 两 端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD。

(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明;
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明。
-
科目: 来源: 题型:
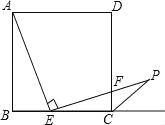
查看答案和解析>>【题目】如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,
(1)
 的值为 ;
的值为 ;(2)求证:AE=EP;
(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家主管部门规定:从2008年6月1日起,各商家禁止向消费者免费提供一次性塑料购物袋.为了了解巴中市市民对此规定的看法,对本市年龄在16—65岁之间的居民,进行了400个随机访问抽样调查,并根据每个年龄段的抽查人数和该年龄段对此规定的支持人数绘制了下面的统计图.

根据上图提供的信息回答下列问题:
(1)被调查的居民中,人数最多的年龄段是 岁.
(2)已知被调查的400人中有83%的人对此规定表示支持,请你求出31—40岁年龄段的满意人数,并补全图b.
(3)比较21—30岁和41—50岁这两个年龄段对此规定的支持率的高低(四舍五入到1%,注:某年龄段的支持率

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,从左到右的变形是因式分解的是( )
A.(x+3y)(x﹣3y)=x2﹣9y2
B.a(x+y+1)=ax+ay+a
C.4x2﹣1=(2x+1)(2x﹣1)
D.a2c﹣a2b+1=a2(c﹣b)+1 -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年响水县某天最高气温为8℃,最低气温为-3℃,那么这天的最高气温比最低气温高 ( )
A. -11℃ B. -7℃ C. 7℃ D. 11℃
相关试题

