搜索
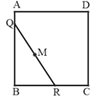
【题目】如图，正方形ABCD的边长为4，将长为4的线段QR的 两 端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时点R从点B出发，沿图中所示方向按B→C→D→A→B滑动到B止，在这个过程中，线段QR的中点M所经过的路线围成的图形的面积为_____________.
参考答案：
【答案】16－4π
【解析】根据题意得点M到正方形各顶点的距离都为2，点M所走的运动轨迹为以正方形各顶点为圆心，以2为半径的四个扇形，
∴点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积。
而正方形ABCD的面积为4×4=16,4个扇形的面积为
=4π，
∴点M所经过的路线围成的图形的面积为164π.
故答案为164π
点睛: 根据直角三角形的性质，斜边上的中线等于斜边的一半，可知：点M到正方形各顶点的距离都为2，故点M所走的运动轨迹为以正方形各顶点为圆心，以2为半径的四个扇形，点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知实数a，b满足a+1>b+1，则下列选项错误的为（ ）
A. a>b B. a+2>b+2 C. –a<–b D. 2a>3b
-
科目： 来源： 题型：
查看答案和解析>>【题目】某射击队要从甲,乙,丙,丁四名队员中选出一名队员代表射击队参加射击比赛,各队员的平时成绩的平均数及方差如表所示:
甲
乙
丙
丁
平均数(环)
9.8
9.3
9.6
9.8
方差(环2)
3.3
3.3
3.5
6.1
根据表中数据,要从这四个队员中选择一个成绩好且发挥稳定的队员去参赛,那么应该选的队员是（ ）
A. 甲B. 乙C. 丙D. 丁
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两同学的家与学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校、乙同学骑自行车去学校．已知甲步行速度是乙骑自行车速度的
，公交车的速度是乙骑自行车速度的2倍．甲乙两同学同时从家发去学校，结果甲同学比乙同学早到2分钟．（1）求乙骑自行车的速度；
（2）当甲到达学校时，乙同学离学校还有多远？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠ACB=2∠B，如图①，当∠C=90°，AD为∠BAC的角平分线时，在AB上截取AE=AC，连接DE，易证AB=AC+CD。
（1）如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明；
（2）如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系?请写出你的猜想，并对你的猜想给予证明。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为3的正方形ABCD中，点E是BC边上的点，BE=1，∠AEP=90°，且EP交正方形外角的平分线CP于点P，交边CD于点F，
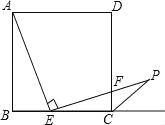
（1）
的值为 ；（2）求证：AE=EP；
（3）在AB边上是否存在点M，使得四边形DMEP是平行四边形？若存在，请给予证明；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图1正方形网格（每个小正方形边长为1）中画出格点△ABC，使AB=AC=5，BC=
(2)在△ABC中， AB、BC、AC三边的长分别为
、、
，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图2所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．①△ABC的面积为： ．
②若△DEF三边的长分别为
、
、
，请在图3的正方形网格中画出相应的△DEF，并利用构图法求出它的面积为_____________．
相关试题
