【题目】在一个不透明的袋子中装有红、黑、白三种球共![]() 个,他们除了颜色外其余完全一样. 已知黑球是白球的
个,他们除了颜色外其余完全一样. 已知黑球是白球的![]() 倍少
倍少![]() 个,将球充分搅匀后,随机摸出一球是红球的概率是
个,将球充分搅匀后,随机摸出一球是红球的概率是![]()
(1)这三种球各有多少个?
(2)随机摸出一球是白球的概率是多少?
(3)若从袋子中拿出![]() 个球(没有红球)后,随机摸一次摸到红球的概率是多少?
个球(没有红球)后,随机摸一次摸到红球的概率是多少?
参考答案:
【答案】(1)红球有30,黑球45,白球有25;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)根据红、黑、白三种颜色球共有的个数乘以红球的概率求出红球的数量,再设白球有x个,得出黑球有(2x-5)个,根据题意列出方程,求出白球的个数,即可解答;
(2)由(1)可知白球的数量,再除以总的球数即可;
(3)先求出取走10个球后,还剩的球数,再根据红球的个数,除以还剩的球数即可.
解:(1)根据题意得:
红球有100×![]() =30,
=30,
设白球有x个,则黑球有(2x-5)个,
根据题意得x+2x-5=100-30
解得x=25.
∴黑球2×25-5=45,
答:红球有30,黑球45,白球有25.
(2)有(1)可知白球有25个,
所以摸出一个球是白球的概率P=![]() ;
;
(3)因为取走10个球后,还剩90个球,其中红球的个数没有变化,
所以从剩余的球中摸出一个球是红球的概率![]() ;
;
-
科目: 来源: 题型:
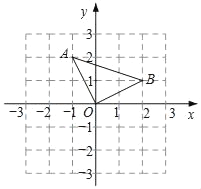
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).
(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)
(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为 ,PA+PB的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第一个
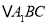 中,
中,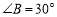 ,
,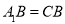 ,在边
,在边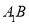 上任取一
上任取一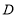 ,延长
,延长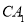 到
到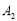 ,使
,使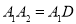 ,得到第
,得到第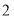 个
个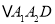 ,在边
,在边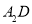 上任取一点
上任取一点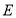 ,延长
,延长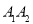 到
到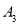 ,使
,使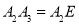 ,得到第三个
,得到第三个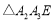 ,…按此做法继续下去,第
,…按此做法继续下去,第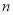 个等腰三角形的底角的度数是________________.
个等腰三角形的底角的度数是________________.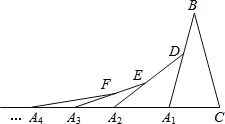
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.
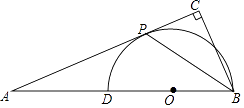
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
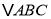 中,
中,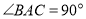 ,
,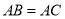 ,
,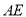 是过
是过 点的一条直线
点的一条直线
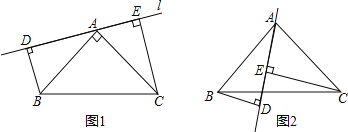
(1)作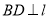 于点
于点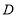 ,
,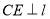
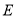 点,若
点,若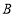 点和
点和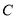 点在直线
点在直线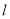 的同侧,求证:
的同侧,求证: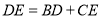 ;
;
(2)若直线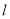 绕点
绕点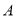 旋转到
旋转到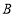 点和
点和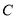 点在其两侧,其余条件不变,问:
点在其两侧,其余条件不变,问: 的关系如何?请予以证明.
的关系如何?请予以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
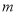 ,
,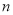 满足等式
满足等式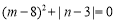 .
.(1)求
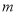 ,
,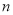 的值;
的值;(2)已知线段
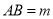 ,在直线
,在直线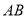 上取一点
上取一点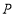 ,恰好使
,恰好使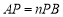 ,点
,点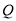 为
为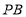 的中点,求线段
的中点,求线段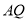 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图时用黑色的正六边形和白色的正方形按照一定的规律组合而成的两色图案

(1)当黑色的正六边形的块数为1时,有6块白色的正方形配套;当黑色的正六边形块数为2时,有11块白色的正方形配套;则当黑色的正六边形块数为3,10时,分别写出白色的正方形配套块数;
(2)当白色的正方形块数为201时,求黑色的正六边形的块数.
(3)组成白色的正方形的块数能否为100,如果能,求出黑色的正六边形的块数,如果不能,请说明理由
相关试题

