【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.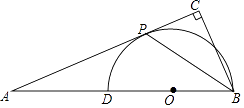
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
参考答案:
【答案】
(1)证明:连接OP,
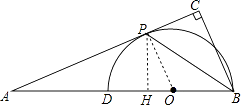
∵AC是⊙O的切线,
∴OP⊥AC,BC⊥AC,
∴OP∥BC,
∴∠OPB=∠PBC,
∵OP=OB,
∴∠OPB=∠OBP,
∴∠PBC=∠OBP,
∴BP平分∠ABC
(2)作PH⊥AB于H.
∵PB平分∠ABC,PC⊥BC,PH⊥AB,
∴PC=PH=1,
在Rt△APH中,AH= ![]() =2
=2 ![]() ,
,
∵∠A=∠A,∠AHP=∠C=90°,
∴△APH∽△ABC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB=3 ![]() ,
,
∴BH=AB﹣AH= ![]() ,
,
在Rt△PBC和Rt△PBH中,
![]() ,
,
∴Rt△PBC≌Rt△PBH,
∴BC=BH= ![]() .
.
【解析】(1) 根据切线的性质易证OP∥BC,由平行线的性质定理得∠OPB=∠PBC,由等边对等角得∠OPB=∠OBP,进而∠PBC=∠OBP,即BP平分∠ABC;(2) 作PH⊥AB于H. 由角平分线的性质定理得PC=PH=1,在Rt△APH中由勾股定理得AH得长 度,进而判断出△APH∽△ABC,再由相似三角形的对应边成比例得出AB的长,进而得出BH的长,再证出Rt△PBC≌Rt△PBH,由全等三角形对应边成比例就可以得出结论。
【考点精析】掌握角平分线的性质定理和勾股定理的概念是解答本题的根本,需要知道定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
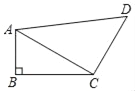
查看答案和解析>>【题目】如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
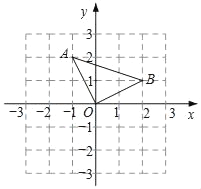
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).
(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)
(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为 ,PA+PB的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第一个
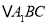 中,
中,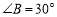 ,
,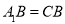 ,在边
,在边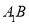 上任取一
上任取一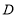 ,延长
,延长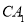 到
到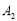 ,使
,使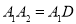 ,得到第
,得到第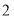 个
个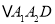 ,在边
,在边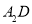 上任取一点
上任取一点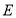 ,延长
,延长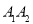 到
到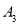 ,使
,使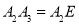 ,得到第三个
,得到第三个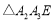 ,…按此做法继续下去,第
,…按此做法继续下去,第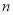 个等腰三角形的底角的度数是________________.
个等腰三角形的底角的度数是________________.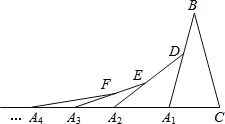
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有红、黑、白三种球共
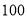 个,他们除了颜色外其余完全一样. 已知黑球是白球的
个,他们除了颜色外其余完全一样. 已知黑球是白球的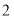 倍少
倍少 个,将球充分搅匀后,随机摸出一球是红球的概率是
个,将球充分搅匀后,随机摸出一球是红球的概率是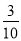
(1)这三种球各有多少个?
(2)随机摸出一球是白球的概率是多少?
(3)若从袋子中拿出
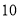 个球(没有红球)后,随机摸一次摸到红球的概率是多少?
个球(没有红球)后,随机摸一次摸到红球的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
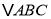 中,
中,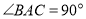 ,
,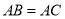 ,
,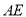 是过
是过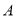 点的一条直线
点的一条直线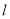
(1)作 于点
于点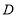 ,
,
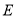 点,若
点,若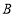 点和
点和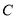 点在直线
点在直线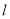 的同侧,求证:
的同侧,求证: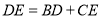 ;
;
(2)若直线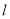 绕点
绕点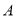 旋转到
旋转到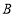 点和
点和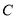 点在其两侧,其余条件不变,问:
点在其两侧,其余条件不变,问: 的关系如何?请予以证明.
的关系如何?请予以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
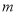 ,
,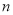 满足等式
满足等式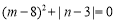 .
.(1)求
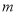 ,
,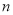 的值;
的值;(2)已知线段
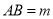 ,在直线
,在直线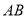 上取一点
上取一点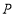 ,恰好使
,恰好使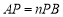 ,点
,点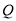 为
为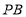 的中点,求线段
的中点,求线段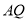 的长.
的长.
相关试题

