【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 是过
是过![]() 点的一条直线
点的一条直线![]()
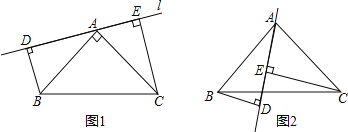
(1)作![]() 于点
于点![]() ,
,![]()
![]() 点,若
点,若![]() 点和
点和![]() 点在直线
点在直线![]() 的同侧,求证:
的同侧,求证:![]() ;
;
(2)若直线![]() 绕点
绕点![]() 旋转到
旋转到![]() 点和
点和![]() 点在其两侧,其余条件不变,问:
点在其两侧,其余条件不变,问:![]() 的关系如何?请予以证明.
的关系如何?请予以证明.
参考答案:
【答案】(1)证明见解析;(2)CE=BD+DE,理由见解析;
【解析】
(1)由AAS证明△ABD≌△CAE,得到BD=AE,AD=CE,即可解决问题.
(2)由AAS证明证明△ABD≌△CAE,得出BD=AE,AD=CE,即可得出结论.
(1)证明:∵∠BAC=90°,BD⊥DE,CE⊥DE,
∴∠DAB+∠DBA=∠DAB+∠EAC,
∴∠DBA=∠EAC;
在△ABD与△CAE中,
 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∴DE=BD+CE.
(2)解:CE=BD+DE;理由如下:
同(1)得:∠ABD=∠CAE,
在△ABD和△CAE中,
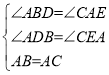 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD=AE+DE,
∴CE=BD+DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第一个
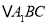 中,
中,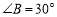 ,
,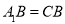 ,在边
,在边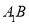 上任取一
上任取一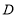 ,延长
,延长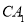 到
到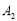 ,使
,使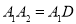 ,得到第
,得到第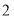 个
个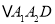 ,在边
,在边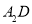 上任取一点
上任取一点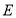 ,延长
,延长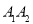 到
到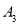 ,使
,使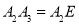 ,得到第三个
,得到第三个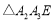 ,…按此做法继续下去,第
,…按此做法继续下去,第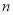 个等腰三角形的底角的度数是________________.
个等腰三角形的底角的度数是________________.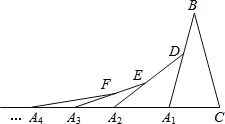
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.
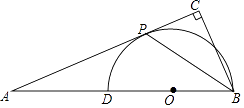
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有红、黑、白三种球共
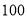 个,他们除了颜色外其余完全一样. 已知黑球是白球的
个,他们除了颜色外其余完全一样. 已知黑球是白球的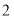 倍少
倍少 个,将球充分搅匀后,随机摸出一球是红球的概率是
个,将球充分搅匀后,随机摸出一球是红球的概率是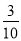
(1)这三种球各有多少个?
(2)随机摸出一球是白球的概率是多少?
(3)若从袋子中拿出
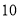 个球(没有红球)后,随机摸一次摸到红球的概率是多少?
个球(没有红球)后,随机摸一次摸到红球的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
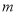 ,
,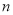 满足等式
满足等式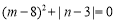 .
.(1)求
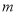 ,
,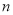 的值;
的值;(2)已知线段
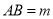 ,在直线
,在直线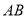 上取一点
上取一点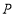 ,恰好使
,恰好使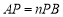 ,点
,点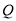 为
为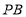 的中点,求线段
的中点,求线段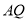 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图时用黑色的正六边形和白色的正方形按照一定的规律组合而成的两色图案

(1)当黑色的正六边形的块数为1时,有6块白色的正方形配套;当黑色的正六边形块数为2时,有11块白色的正方形配套;则当黑色的正六边形块数为3,10时,分别写出白色的正方形配套块数;
(2)当白色的正方形块数为201时,求黑色的正六边形的块数.
(3)组成白色的正方形的块数能否为100,如果能,求出黑色的正六边形的块数,如果不能,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是两位同学的一段对话:
聪聪:周末我们去国家博物馆参观“伟大的变革﹣﹣庆祝改革开放40周年大型展览”吧.
明明:好啊,我家离国家博物馆约30km,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢.
聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km,坐公交车,你出发40分钟后我再出发就能和你同时到达.
根据对话内容,请你求出公交车和地铁的平均行驶速度.
相关试题

