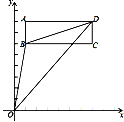
【题目】如图,在长方形ABCD中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出点D的坐标;
(2)连接线段OB,OD,BD,请求出△OBD的面积;
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,设运动的时间为t秒,是否存在某一时刻,使△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)D(7,8);(2)17;(3)![]() ;
;
【解析】
(1)根据长方形的性质得出AB=DC,AD=BC,求出AD∥x轴,AB∥DC∥y轴,即可得出D的坐标;
(2)延长AB交x轴于M,延长DC交x轴于N,求出OM=1,BM=6,DN=8,NM=AD=6,ON=7,求出![]() ,代入求出即可.
,代入求出即可.
(3)存在某一时刻,△OBD的面积与长方形ABCD的面积相等,分为两种情况:①当在第一象限内时,作AE⊥y轴,根据![]() 代入求出即可;②当在第四象限时,作BM⊥y轴于M,根据
代入求出即可;②当在第四象限时,作BM⊥y轴于M,根据![]() 代入求出即可.
代入求出即可.
(1)∵四边形ABCD是长方形,
∴AB=DC,AD=BC,
∵点A(1,8),B(1,6),C(7,6).
∴AD∥x轴,AB∥DC∥y轴,
∴D的坐标是(7,8);
(2)延长AB交x轴于M,延长DC交x轴于N.
∵A(1,8),B(1,6),C(7,6),D(7,8),
∴OM=1,BM=6,DN=8,NM=AD=7-1=6,ON=7.
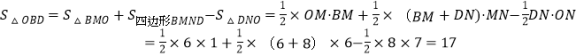
(3)存在某一时刻,△OBD的面积与长方形ABCD的面积相等,分两种情况:
①当在第一象限内时,作AE⊥y轴于E, 则![]() ,则由:
,则由:![]() ,
,![]() ,解得:t=
,解得:t=![]() ,
,
②当在第四象限时,作BM⊥y轴于M,则有![]() .
.
∴![]() .
.
综上,当 ![]() ,△OBD的面积与长方形ABCD的面积相等.
,△OBD的面积与长方形ABCD的面积相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过四边形的一个顶点可以画一条对角线,且把四边形分成两个三角形;过五边形的一个顶点可以画两条对角线,且把五边形分成三个三角形;......猜想:过n边形的一个顶点可以画_________条对角线,且把n边形分成 _________个三角形.
-
科目: 来源: 题型:
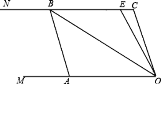
查看答案和解析>>【题目】如图,已知两条射线OM∥CN,动线段AB的两个端点A,B分别在射线OM,CN上,且∠C=∠OAB=108°,点E在线段CB上,OB平分∠AOE.
(1)图中有哪些与∠AOC相等的角?并说明理由;
(2)若平移AB,那么∠OBC与∠OEC的度数比是否随着AB位置变化而变化?若变化,找出变化规律;若不变,求出这个比值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.

(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
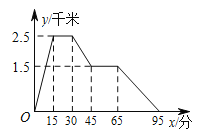
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2_______∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2=______.
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°- = ,猜想∠BDA+∠CEA与∠A的关系为

-
科目: 来源: 题型:
查看答案和解析>>【题目】商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出销售单价提高 元与总的销售利润y元之间的函数关系式;
元与总的销售利润y元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
相关试题

