【题目】商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出销售单价提高 ![]() 元与总的销售利润y元之间的函数关系式;
元与总的销售利润y元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
参考答案:
【答案】
(1)解:当销售单价提高x元时,销售量减少了 ![]() 个,
个,
此时单价为(50+x)元,销售量为(30- ![]() )个
)个
则x与y的函数关系式为:y=(50+x-40)(30- ![]() )(0≤ x ≤150)
)(0≤ x ≤150)
答:x与y的函数关系式为:y=(50+x-40)(30- ![]() )(0≤ x ≤150);
)(0≤ x ≤150);
(2)解:将(1)中函数整理后,得:
y=- ![]() +28 x+300=-
+28 x+300=- ![]()
∵- ![]() <0
<0
∴二次函数y=- ![]() +28 x+300有最大值
+28 x+300有最大值
当x=70时,y有最大值,
此时y=1280,
这种书包的单价为:50+70=120
答:当这种书包的单价为120元时,每月的销售利润最大为1280元。
【解析】(1)当销售单价提高x元时,销售量减少了 ![]() 个,此时单价为(50+x)元,销售量为(30-
个,此时单价为(50+x)元,销售量为(30- ![]() )个 ,根据总利润=单个利润×销售数量得出,y与x之间的函数关系式;
)个 ,根据总利润=单个利润×销售数量得出,y与x之间的函数关系式;
(2)为使每月的销售利润最大,求解求函数的最大值问题,把y与x的函数关系式整理成一般形式,然后配成顶点式,根据顶点式从而得出 ,当x=70时,y有最大值,此时y=1280,这种书包的单价为:50+70=120 。
-
科目: 来源: 题型:
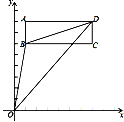
查看答案和解析>>【题目】如图,在长方形ABCD中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出点D的坐标;
(2)连接线段OB,OD,BD,请求出△OBD的面积;
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,设运动的时间为t秒,是否存在某一时刻,使△OBD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )
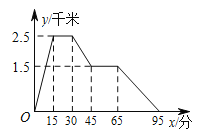
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2_______∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2=______.
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°- = ,猜想∠BDA+∠CEA与∠A的关系为

-
科目: 来源: 题型:
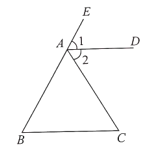
查看答案和解析>>【题目】根据图形及题意填空,并在括号里写上理由.
己知:如图,
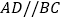 ,
,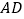 平分
平分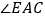 .
.试说明:
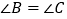 .
.解:因为
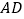 平分
平分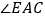 (已知)
(已知)所以
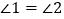 (角平分线的定义)
(角平分线的定义)因为
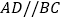 (已知)
(已知)所以∠_________=∠__________(________)
∠____________=∠_________(___________)
所以
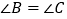 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线a∥b,直线c与直线a、b分别相交于C、D两点,直线d与直线a、b分别相交于A、B两点,点P在直线AB上运动(不与A、B两点重合).
(1)如图1,当点P在线段AB上运动时,总有:∠CPD=∠PCA+∠PDB,请说明理由;
(2)如图2,当点P在线段AB的延长线上运动时,∠CPD、∠PCA、∠PDB之间有怎样的数量关系,并说明理由;
(3)如图3,当点P在线段BA的延长线上运动时,∠CPD、∠PCA、∠PDB之间又有怎样的数量关系(只需直接给出结论)?

相关试题

