【题目】已知,如图点P是△ABC的边BC上的一动点,点E与点P关于直线AB成轴对称,连接EP交AB于点F,连接AP、EC相交于点O,连接AE.

(1)判断AE与AP的数量关系,并说明理由.
(2)在点P的运动过程中,当AE∥BC时,判断AP与BP的数量关系,并说明理由.
(3)若∠BAC=900,点P在运动过程中是否存在线段AP与线段EC互相平分的情况,若存在,请求出点P的位置;若不存在,请说明理由.
参考答案:
【答案】(1)相等,理由见解析;(2)相等,理由见解析;(3)存在,点P为BC的中点时,理由见解析
【解析】
(1)根据SAS证明△AEF≌△APF,再由全等三角形的面积得到AE=AP;
(2)由AE//BC可得∠EAB=∠B,由(1)可得∠EAB=∠BAP,所以∠B=∠BAP,再根据等角对等边得BP=AP;
(3)当点P为BC的中点时,由直角三角形的斜边中点可得BP=CP=AP,从而得到∠B=∠BAP,又由(1)可得AE=AP=PB=PC和∠EAB=∠BAP,则∠B=∠EAB,再得到AE//BC,再根据一组对边平行且相等可得四边形AEPC为平行四边形,由平行四边形的性质可得AP和EC互相平分.
(1)∵点E与点P关于直线AB成轴对称,
∴AB⊥EP且平分,
∴∠AFE=∠AFP,EF=PF,
在△AEF和△APF中,
 ,
,
∴△AEF≌△APF,
∴AE=AP;
(2)如图所示:

∵AE//BC,
∴∠EAB=∠B,
∵△AEF≌△APF,
∴∠EAB=∠BAP,
∴∠B=∠BAP,
∴BP=AP;
(3)存在,当点P为BC的中点时,
∵P是BC的中点,∠BAC=90o,
∴BP=PC=AP,
∴∠B=∠BAP,
由(1)中△AEF≌△APF,
∴∠EAB=∠BAP,AE=AP,
∴∠B=∠EAB,AE=AP=BP=PC,
∴AE//PC,AE=PC,
∴四边形AEPC是平行四边形,
∴AP和CE互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.

(1)如图①,求证:ED为⊙O的切线;
(2)如图②,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元)
2
种植树木利润y1(万元)
4
种植花卉利润y2(万元)
2
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示.在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,如果点P在线段BC上以3cm/s的速度由点B向点C运动,同时点Q在线段CA上由点C向点A运动.

(1)若点Q与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q与点P的运动速度不同,当点Q的运动速度是多少时能使△BPD与△CQP全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF、CF.

(1)如图1, 当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=
 ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx-2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=-2和x=5时二次函数的函数值y相等.

(1)求实数a,b的值;
(2)如图①,动点E,F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒
 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由;
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解八年级学生对
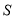 (科学)、
(科学)、 (技术)、
(技术)、 (工程)、
(工程)、 (艺术)、
(艺术)、 (数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
(数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
(1)这次抽样调查共调查了多少名学生?
(2)补全条形统计图;
(3)求扇形统计图中
 (数学)所对应的圆心角度数;
(数学)所对应的圆心角度数;(4)若该校八年级学生共有400人,请根据样本数据估计该校八年级学生中对
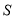 (科学)最感兴趣的学生大约有多少人?
(科学)最感兴趣的学生大约有多少人?
相关试题

