【题目】如图所示,AB是☉O的弦,C,D为弦AB上两点,且OC=OD,延长OC,OD,分别交☉O于点E,F.

试证: ![]() =
=![]() .
.
参考答案:
【答案】证明见解析
【解析】试题分析:根据等腰三角形的性质由OC=OD得∠OCD=∠ODC,由OA=OB得∠A=∠B,再根据三角形外角性质得∠OCD=∠A+∠AOC,∠ODC=∠B+∠BOD,利用等量代换得到∠AOC=∠BOD,然后根据在同圆和等圆中,相等的圆心角所对的弧相等即可得到结论.
证明:∵OC=OD,∴∠OCD=∠ODC.
∵AO=OB,∴∠A=∠B.
∴∠OCD-∠A=∠ODC-∠B,
即∠AOC=∠BOD,
即∠AOE=∠BOF.∴![]() =
=![]() .
.
点睛:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于点D,AE平分∠BAC,求∠EAD的度数;
(2)将(1)中“∠B=40°,∠C=80°”改为“∠B=x°,∠C=y°,∠C>∠B”,
①其他条件不变,你能用含x,y的代数式表示∠EAD吗?请写出,并说明理由;
②如图②,AE平分∠BAC,F为AE上一点,FM⊥BC于点M,用含x,y的代数式表示∠EFM,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x、y的方程(a﹣2)x|a|﹣1+2y=3是二元一次方程,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在-4,2,-1,3这四个数中,比-2小的数( )
A.-4B.2C.-1D.3
-
科目: 来源: 题型:
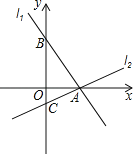
查看答案和解析>>【题目】如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=
 .
.(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次不等式解实际问题
为鼓励市民节约用水,某自来水公司规定:若每户用水不超过5m3,收费标准为1.8元/m3,若每用户用水量超过5m3,则超出部分的收费标准是2元/m3,若小颖家每月水费都不超过11元,求小颖家每月用水量最多是多少.
相关试题

