搜索
【题目】列一元一次不等式解实际问题
为鼓励市民节约用水，某自来水公司规定：若每户用水不超过5m3，收费标准为1.8元/m3，若每用户用水量超过5m3，则超出部分的收费标准是2元/m3，若小颖家每月水费都不超过11元，求小颖家每月用水量最多是多少．
参考答案：
【答案】小颖家每月用水量最多是6m3．
【解析】
设小颖家每月用水量为xm3，根据每月的水费＝1.8×5+2×超出5m3的部分结合小颖家每月水费都不超过11元，即可得出关于x的一元一次不等式，解之取其中的最大值即可得出结论．
设小颖家每月用水量为xm3，
依题意，得：1.8×5+2（x﹣5）≤11，
解得：x≤6．
答：小颖家每月用水量最多是6m3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示,AB是☉O的弦,C,D为弦AB上两点,且OC=OD,延长OC,OD,分别交☉O于点E,F.
试证:
=
. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，过点A（2，0）的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB=
．（1）求点B的坐标；
（2）若△ABC的面积为4，求直线l2的解析式．
-
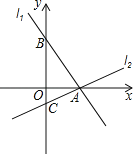
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，在ABCD中，E，F分别是边AD，BC上的点，且AE=CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点O．
（1）求证：△ABE≌△CDF；
（2）连接DG，若DG=BG，则四边形BEDF是什么特殊四边形？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在-2、5、-6、-7这四个数中，任取两个数相乘，得到的积最小的是（ ）
A.42B.-35C.-30D.-10
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．
（1）求证：△ABQ≌△CAP；
（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．
（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，直接写出它的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,∠AOB=90°,C,D是
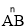的三等分点,AB分别交OC,OD于点E,F.试找出图中相等的线段(半径除外).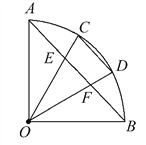
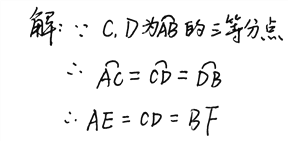
(1)错因: .
(2)纠错:____________________________________________________________
.
相关试题
