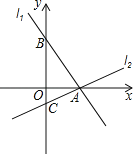
【题目】如图，过点A（2，0）的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB=
．
（1）求点B的坐标；
（2）若△ABC的面积为4，求直线l2的解析式．
【答案】（1）点B的坐标为（0，3）；（2）l2的解析式为y=
x-1.
【解析】（1）先根据勾股定理求得BO的长，再写出点B的坐标；（2）先根据△ABC的面积4，求得CO的长，再根据点A、C的坐标运用待定系数法求得直线l2的解析式.
解：（1）∵点A（2，0），AB=
∴BO=
=3
∴点B的坐标为（0，3）；
（2）∵△ABC的面积为4 ∴×BC×AO=4 ∴×BC×2=4，即BC=4
∵BO=3 ∴CO=4﹣3=1 ∴C（0，﹣1）
设l2的解析式为y=kx+b，则
，解得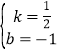
，
∴l2的解析式为y=x﹣1．
“点睛”本题主要考查了两条直线的交点问题，解题的关键是掌握勾股定理以及待定系数法.注意：两条直线的交点坐标，就是由这两条直线相对应的一次函数的表达式所组成二元一次过程组的解，反之也成立.
科目：初中数学 来源： 题型：
【题目】如图所示，AB⊥BC，CD⊥BC，垂足分别为B、C，AB=BC，E为BC的中点，且AE⊥BD于F，若CD=4cm，则AB的长度为（ ）
A. 4cm B. 8cm C. 9cm D. 10cm
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：直线AB∥CD，点M，N分别在直线AB，CD上，点E为平面内一点.
(1)如图1，∠BME，∠E，∠END的数量关系为 (直接写出答案)；
(2)如图2，∠BME＝m°，EF平分∠MEN，NP平分∠END，EQ∥NP，求∠FEQ的度数(用用含m的式子表示)
(3)如图3，点G为CD上一点，∠BMN＝n·∠EMN，∠GEK＝n·∠GEM，EH∥MN交AB于点H，探究∠GEK，∠BMN，∠GEH之间的数量关系(用含n的式子表示)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线与x轴交于A（﹣1，0）、B（4，0）两点，与y轴交于点C（0，3）．
（1）求抛物线的解析式；
（2）在x轴下方的抛物线上是否存在一点P，使△PAB的面积等于△ABC的面积？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解全校学生上学期参加社区活动的情况，学校随机调查了本校50名学生参加社区活动的次数，并将调查所得的数据整理如下：
参加社区活动次数的频数、频率分布表
根据以上图表信息，解答下列问题：
（1）表中a= ，b= ；
（2）请把频数分布直方图补充完整（画图后请标注相应的数据）；
（3）若该校共有1200名学生，请估计该校在上学期参加社区活动超过6次的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,∠AOB=90°,C,D是
的三等分点,AB分别交OC,OD于点E,F.试找出图中相等的线段(半径除外).
(1)错因: .
(2)纠错:____________________________________________________________
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=a(x2)2+3的图象经过点(1,0).
(1)求这个二次函数的解析式；
(2)分别指出这个二次函数图象的开口方向、对称轴和顶点坐标.
(3) 写出把此抛物线向右平移1个单位长度，再向上平移2个单位长度后的抛物线解析式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
