【题目】(1)如图①,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于点D,AE平分∠BAC,求∠EAD的度数;
(2)将(1)中“∠B=40°,∠C=80°”改为“∠B=x°,∠C=y°,∠C>∠B”,
①其他条件不变,你能用含x,y的代数式表示∠EAD吗?请写出,并说明理由;
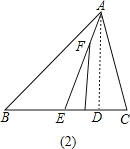
②如图②,AE平分∠BAC,F为AE上一点,FM⊥BC于点M,用含x,y的代数式表示∠EFM,并说明理由.

参考答案:
【答案】(1)∠EAD=20°;(2)①∠EAD=![]() y-
y-![]() x,理由见解析;②∠EFM=
x,理由见解析;②∠EFM=![]() y-
y-![]() x,理由见解析.
x,理由见解析.
【解析】试题分析:(1)根据三角形内角和定理求出∠BAC,求出∠CAE,根据三角形内角和定理求出∠CAD,代入∠EAD=∠CAE-∠CAD求出即可;
(2)根据三角形内角和定理求出∠BAC,求出∠CAE,根据三角形内角和定理求出∠CAD,代入∠EAD=∠CAE-∠CAD求出即可;
(3)根据三角形内角和定理求出∠BAC,求出∠CAE,根据三角形内角和定理求出∠CAD,代入∠EAD=∠CAE-∠CAD求出∠EAD,推出∠FEM=∠EAD,即可得出答案.
试题解析:(1)∵∠B=40°,∠C=80°,
∴∠BAC=180°-∠B-∠C=60°,
∵AE平分∠BAC,
∴∠CAE=![]() ∠BAC=30°,
∠BAC=30°,
∵AD⊥BC,
∴∠ADC=90°,
∵∠C=80°,
∴∠CAD=90°-∠C=10°,
∴∠EAD=∠CAE-∠CAD=30°-10°=20°;
(2)∵三角形的内角和等于180°,
∴∠BAC=180°-∠B-∠C=180°-x-y,
∵AE平分∠BAC,
∴∠CAE= ![]() ∠BAC=
∠BAC= ![]() (180°xy),
(180°xy),
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°-y,
∴∠EAD=∠CAE-∠CAD= ![]() (180°-x-y)-(90°-y)=
(180°-x-y)-(90°-y)=![]() y-
y-![]() x;
x;
(3)过A作AD⊥BC于D,
∵三角形的内角和等于180°,
∴∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠CAE= ![]() ∠BAC=
∠BAC= ![]() (180°x-y),
(180°x-y),
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°-y,
∴∠EAD=∠CAE-∠CAD= ![]() (180°-x-y)-(90°-y)=
(180°-x-y)-(90°-y)= ![]() y-
y-![]() x,
x,
∵AD⊥BC,FM⊥BC,
∴AD∥FM,
∴∠EFM=∠EAD,
∴∠EFM= ![]() y-
y-![]() x.
x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1) 是描述小凡的运动过程(填
 或
或 );
);(2)小凡和小光先出发的是 ,先出发了 分钟;
(3)小凡与小光先到达图书馆的是 ,先到了 分钟;
(4)求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣1,2)是由点Q(0,﹣1)经过( )而得到的.
A.先向右平移1个长度,再向下平移3个单位长度
B.先向左平移1个长度,再向下平移3个单位长度
C.先向上平移3个长度,再向左平移1个单位长度
D.先向下平移1个长度,再向右平移3个单位长度
-
科目: 来源: 题型:
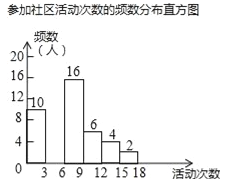
查看答案和解析>>【题目】某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率分布表

根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x、y的方程(a﹣2)x|a|﹣1+2y=3是二元一次方程,则a=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在-4,2,-1,3这四个数中,比-2小的数( )
A.-4B.2C.-1D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AB是☉O的弦,C,D为弦AB上两点,且OC=OD,延长OC,OD,分别交☉O于点E,F.

试证:
 =
= .
.
相关试题

