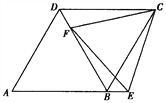
【题目】如图,在菱形ABCD中,点F为对角线BD上一点,点E为AB的延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.
参考答案:
【答案】(1)证明见解析;(2)∠CFE=60°.
【解析】(1)根据菱形的性质得出CD=CB,又DF=BE,CF=CE,根据SSS即可证明△CFD≌△CEB;
(2)根据全等三角形、菱形的性质得出∠ABD=∠CBD=∠CDB=∠CBE,由平角的定义求出∠ABD=∠CBD=60°,再证明∠FCE=60°,那么由CF=CE,得出△AFE是等边三角形,于是∠CFE=60°.
证明:(1)∵四边形 ABCD是菱形,∴CD=CB.
在△CFD和△CEB中, 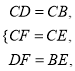 ∴△CFD≌△CEB.
∴△CFD≌△CEB.
(2)∵△CFD≌△CEB,∴∠CDB=CBE, ∠DCF=∠BCE.∵CD=CB,
∴∠CDB=∠CBD,∴∠ABD=∠CBD=∠CBE=60°,∴∠DCB=60°,
∴∠FCE=∠FCB+∠BCE=∠FCB+∠DCF=60°.
又CF=CE,∴△CFE为等边三角形,∴∠CFE=60°.
“点睛”本题考查了菱形的性质:①菱形具有平行四边形的一般性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了全等三角形、等边三角形的判定与性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(1,1)先向左平移2个单位长度,再向下平移3个单位长度得到点B,则点B的坐标是______.
-
科目: 来源: 题型:
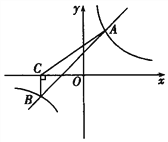
查看答案和解析>>【题目】如图,一次函数
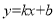 与反比例函数
与反比例函数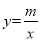 的图象交于A(2,4)、B(-4,
的图象交于A(2,4)、B(-4, 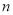 )两点.
)两点.(1)分别求出一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式
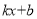 >
>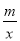 的解集;
的解集;(3)过点B作BC⊥x轴,垂足为C,连接AC,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
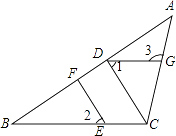
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,试判断DG与BC的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】若x=m是方程x2+2x-2019=0的一个根,则m(m+2)的值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组长度的线段能构成三角形的是( )
A. 1.5cm 3.9cm 2.3cm B. 3.5cm 7.1cm 3.6cm
C. 6cm 1cm 6cm D. 4cm 10cm4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
相关试题

